Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB =

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = a, OC = 2a. Gọi M là trung điểm của AB. Khoảng cách giữa đường thẳng OM và AC bằng

• A.

  A. $\large \dfrac{\sqrt{2}a}{3}$

• B.

  B. $\large \dfrac{2\sqrt{5}a}{5}$

• C.

  C. $\large \dfrac{\sqrt{2}a}{2}$

• D.

  D. $\large \dfrac{2a}{3}$

Chọn D

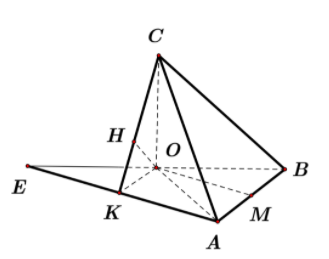
Dựng $\large AE//OM$, khi đó: $\large OM//(CAE)$. Do đó: $\large d(OM, AC)=d(OM, (CAE))=d(O, (CAE))$

Dựng $\large OK\perp AE$, ta có: 

$\large \left\{\begin{align}& AE\perp OK\\& AE\perp OC\,\, (\text { Vì}\,\, CO \perp (ABC))\\\end{align}\right. $ $\large \Rightarrow AE\perp (COK)$ 

Mà $\large AE \subset (CAE)$ nên $\large (CAE)\perp (COK)$

Ta có: $\large (CAE)\cup (COK)=CK$. Kẻ $\large OH\perp CK$, khi đó: $\large OH\perp (COK)$

Suy ra: $\large d(O, (CAE))=OH$

Xét tam giác OAB ta có: $\large AB=\sqrt{OA^2+OB^2}=a\sqrt{2}$

Dễ thấy OKAM là hình chữ nhật nên $\large OK=AM=\dfrac{AB}{2}=\dfrac{a\sqrt{2}}{2}$

Xét tam giác COK ta có: 

$\large \dfrac{1}{OH^2}=\dfrac{1}{OK^2}+\dfrac{1}{OC^2}\Rightarrow \dfrac{1}{OH^2}=\dfrac{1}{\left(\dfrac{a\sqrt{2}}{2}\right)^2}+\dfrac{1}{(2a)^2}\Rightarrow OH=\dfrac{2}{3}a$