Từ hình vuông có cạnh bằng 6 người ta cắt bỏ các tam giác vuông cân tạ

Từ hình vuông có cạnh bằng 6 người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp bằng

• A.

  A. $\large 8\sqrt{2}$

• B.

  B. $\large 9\sqrt{2}$

• C.

  C. $\large 10\sqrt{2}$

• D.

  D. $\large 11\sqrt{2}$

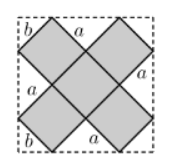
Gọi độ dài các cạnh của hình hộp chữ nhật không nắp là $\large a,b$ (như hình vẽ). 

Suy ra hình chữ nhật có đáy là hình vuông cạnh $\large b$, chiều cao bằng $\large a\longrightarrow V_{kk}=ab^{2}$

Ta tính được cạnh của hình vuông ban đầu là $\large b\sqrt{2}+a\sqrt{2}$

Theo đề suy ra $\large b\sqrt{2}+a\sqrt{2}=6\longrightarrow a=3\sqrt{2}-b$

Khi đó $\large V_{kk}=ab^{2}=(3\sqrt{2}-b).b^{2}$

Xét hàm $\large f(b)=3\sqrt{2}b^{2}-b^{3}$ trên $\large (0 ; 3\sqrt{2})$, ta được $\large\underset{(0;3\sqrt{2})}{max}f(x)=f(2 \sqrt{2})=8 \sqrt{2}$

Đáp án A