Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích $

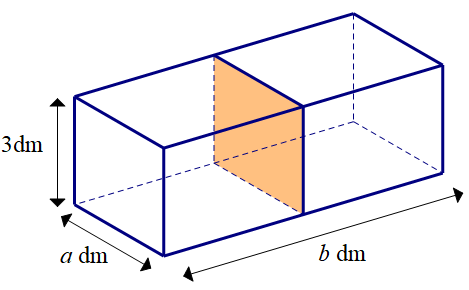
Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích $\large 72dm^{2}$ và chiều cao là $\large 3dm$. Một vách ngăn (cũng bằng kính) ở giữa chia bể cá thành hai ngăn, với các kích thước $\large a,b$ (đơn vị dm) như hình vẽ. Tính $\large a,b$ để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bề dày các tấm kính như nhau và không ảnh hưởng tới thể tích bể.

• A.

  A. $\large a=\sqrt{24};b=\sqrt{24}$

• B.

  B. $\large a=3;b=8$

• C.

  C. $\large a=3\sqrt{2};b=4\sqrt{2}$

• D.

  D. $\large a=4;b=6$

Có $\large V=72\Leftrightarrow 3.ab=72\Leftrightarrow a=\frac{24}{b}$ (1)

Bể cá tốn ít nguyên liệu nhất nghĩa là diện tích toàn phần nhỏ nhất.

Ta có diện tích toàn phần của bể các là $\large S_{tp}=3.3a+ab+2.b.3=\frac{216}{b}+6b+24$

Áp dụng bất đẳng thức Cosi: $\large S_{tp}=\frac{216}{b}+6b+24\geq 2\sqrt{\frac{216}{b}\cdot 6b}+24=96$

Dấu bằng xảy ra khi và chỉ khi $\large\frac{216}{b}=6b\Leftrightarrow b=6(b>0)$

Từ (1), ta suy ra $\large a=4$

Đáp án D