Cho lăng trụ $\large ABC.A'B'C'$ có đáy là tam giác đều cạnh $\large a

Cho lăng trụ $\large ABC.A'B'C'$ có đáy là tam giác đều cạnh $\large a$. Điểm $\large A'$ cách đều ba điểm $\large A,B,C$. Góc giữa $\large AA'$ và mặt phẳng $\large (ABC)$ bằng $\large 60^{\circ}$.Tính theo $\large a$ khoảng cách $\large h$ giữa hai đường thẳng $\large A'B$ và $\large CC'$

• A.

  A. $\large h=\frac{a\sqrt{13}}{13}$

• B.

  B. $\large h=\frac{3a\sqrt{13}}{13}$

• C.

  C. $\large h=\frac{2a\sqrt{13}}{13}$

• D.

  D. $\large h=\frac{2a\sqrt{39}}{13}$

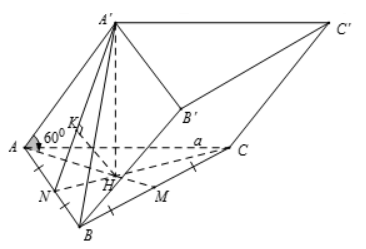
Gọi $\large H$ là trọng tâm tam giác $\large ABC$ và $\large M$ là trung điểm của $\large BC$, khi đó $\large A'.ABC$ là hình chóp đều 

Suy ra  $\large A^{\prime}H\perp(ABC)\Rightarrow\left(AA^{\prime},(ABC)\right)=\widehat{A^{\prime} AH}=60^{\circ}$

Tam giác $\large ABC$ đều cạnh $\large a$ nên $\large\Rightarrow AH=\frac{a\sqrt{3}}{3}\Rightarrow A^{\prime}H=AH.\tan \widehat{A^{\prime}AH}=\frac{a\sqrt{3}}{3}\tan 60^{\circ}=a$

Ta có $\large CC^{\prime}//AA^{\prime}\Rightarrow CC^{\prime}// \left(ABB'A^{\prime}\right)\Rightarrow d\left(A^{\prime}B,CC^{\prime}\right)=d\left(CC^{\prime},\left(ABB'A^{\prime}\right)\right)=d\left(C,\left(ABB'A^{\prime}\right)\right)$ (1)

Gọi $\large CH\bigcap\left(ABB'A^{\prime}\right)=\{N\}\Rightarrow d\left(C,\left(ABB'A^{\prime}\right)\right)=\frac{CN}{HN}.d\left(H,\left(ABB'A^{\prime}\right)\right)=3d\left(H,\left(ABB'A^{\prime}\right)\right)$ (2)

Dựng $\large HK\perp A^{\prime}N\left(K\in A^{\prime}N\right)$, khi đó $\large\Rightarrow d\left(H,\left(ABB'A^{\prime}\right)\right)=HK$ (3) Ta có:

$\large HN=\frac{1}{3} CN=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$.

Xét tam giác $\large A'NH$ ta có:

$\large\frac{1}{HK^{2}}=\frac{1}{A^{\prime} H^{2}}+\frac{1}{HN^{2}}=\frac{1}{a^{2}}+\frac{12}{a^{2}}=\frac{13}{a^{2}} \Rightarrow HK=\frac{a \sqrt{13}}{13}$

Từ (1) , (2) và (3) suy ra $\large h=d\left(A^{\prime} B,CC^{\prime}\right)=\frac{3a\sqrt{13}}{13}$

Đáp án B