Bên trong một căn nhà bỏ hoang hình lập phương thể tích $\Large 1000m^

Bên trong  một căn nhà bỏ hoang hình lập phương thể tích $\Large 1000m^{3}$ có 3 chú nhện rất hay cãi vã nên phải sống riêng. Mùa đông đến, vì đói rét nên chúng đành quyết định hợp tác giăng lưới để bắt mồi. Ba chú nhện tính toán sẽ giăng một mảnh lưới hình tam giác theo cách sau: Mỗi chú nhện sẽ đứng ở mép tường bất kì (có thể mép giữa 2 bức tường, giữa tường với trần hoặc giữa tường với nền) rồi phóng những sợi tơ làm khung đến vị trí cũng của 2 con nhện còn lại rồi sau đó mới phóng tơ đính đan phần lưới bên trong. Nhưng vì vốn đã có hiềm khích từ lâu, nên trước khi bắt đầu, chúng quy định để tránh xô xát, không có bất kì 2 con nhện nào cùng nằm trên 1 mặt tường, nền hoặc trần nhà. Tính chu vi nhỏ nhất của mảnh lưới được giăng (biết các sợi tơ khung căng và không nhún).

• A.

  A. $\large 15\sqrt{6}$ mét 

• B.

  B. $\large 2\sqrt{30}$ mét 

• C.

  C. $\large 12\sqrt{10}$ mét 

• D.

  D. $\large 10\sqrt{2}$ mét 

Bài toán này ta sẽ giải quyết bằng cách ứng dụng phương pháp tọa độ trong không gian

Đặt hệ trục tọa độ như hình vẽ. Không mất tính tổng quát và dựa vào yêu cầu về vị trí 3 con nhện ta xác định là các điểm $\large M,N,P$ nằm trên các cạnh $\large A'B',CC',AD$ như hình vẽ

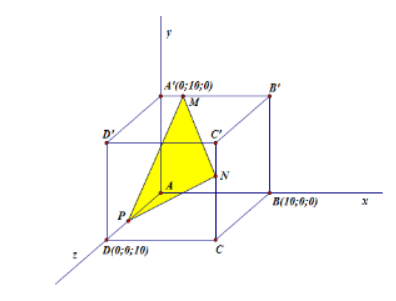
Yêu cầu bài toán là cần tìm tọa độ của 3 điểm $\large M,N,P$ để chu vi tam giác $\large MNP$ nhỏ nhất.

Đặt $\large M(x;10;0),N(10;y;10),P(0;0;z)$. Chu vi ta,m giác $\large MNP$ là:

$\large MN+NP+PM=\sqrt{(x-10)^{2}+(y-10)^{2}+10^{2}}+\sqrt{10^{2}+y^{2}+(z-10)^{2}}+\sqrt{x^{2}+10^{2}+z^{2}}=\sqrt{(10-x)^{2}+(y-10)^{2}+10^{2}}+\sqrt{y^{2}+(z-10)^{2}+10^{2}}+\sqrt{z^{2}+(-x)^{2}+10^{2}}$

Áp dụng bất đẳng thức vecto:

$\large\Rightarrow MN+NP+PM\geq \sqrt{(10-x+y)^{2}+(y+z-20)^{2}+20^{2}}+\sqrt{z^{2}(-x)^{2}+10^{2}}\geq \sqrt{(10-x+y+z)^{2}+(y-10+z-10-x)^{2}+(10+10+10)^{2}}$

$\large =\sqrt{2(y+z-x-5)^{2}+450+(10+10+10)^{2}}\geq 15\sqrt{6}$

Dấu bằng xảy ra khi $\large\left\{\begin{matrix}y+z-x=5\\ \frac{10-x}{y}=\frac{y-10}{z-10}=\frac{10}{10}\\ \frac{10-x+y}{z}=\frac{y+z-20}{-x}=\frac{20}{10}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}y=z\\ 2y-x=5\\ x+y=10\end{matrix}\right.\Leftrightarrow x=y=z=5$

Vậy giá trị cần tìm là $\Large 15\sqrt{6}$

Đáp án A