Trong không gian Oxyz, cho mặt phẳng $\Large (P): x-2y+z+7=0$ và mặt c

Trong không gian Oxyz, cho mặt phẳng $\Large (P): x-2y+z+7=0$ và mặt cầu $\Large (S): x^2+y^2+z^2-2x+4z-10=0$. Gọi (Q) là mặt phẳng song song với mặt phẳng (P) và cắt mặt cầu (S) theo một giao tuyến là đường tròn có chu vi bằng $\Large 6\pi$. Hỏi (Q) đi qua điểm nào trong số các điểm sau?

• A. $\Large (-2; -1; 5).$
• B. $\Large (4; -1; -2).$
• C. $\Large (6; 0; 1).$
• D. $\Large (-3; 1; 4).$

Chọn A

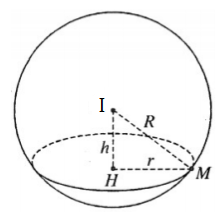
Vì (Q) là mặt phẳng song song với mặt phẳng (P) nên phương trình mặt phẳng (Q) có dạng $\Large x-2y+z+D=0 (D \neq 7)$.

Ta có chu vi đường tròn giao tuyến là $\Large 2\pi r=6\pi \Rightarrow r=3$.

Mặt cầu (S) có tâm $\Large I(1; 0; -2)$ và bán kính $\Large R=\sqrt{15}$.

Suy ra $\Large d\big(I, (Q)\big)=\sqrt{R^2-r^2}=\sqrt{15-9}=\sqrt{6}$.

Do đó $\Large \dfrac{|1-2.0+(-2)+D|}{\sqrt{1^2+(-2)^2+1^2}}=\sqrt{6} \Leftrightarrow |D-1|=6$ $\Large \Leftrightarrow \left[\begin{align} & D=7 (ktm) \\ & D=-5 (tm) \end{align}\right.$.

Suy ra phương trình mặt phẳng (Q) là $\Large x-2y+z-5=0$.

Xét điểm $\Large A(-2; -1; 5)$.

Ta có $\Large -2-2.(-1)+5-5=0$ (đúng).

Vậy (Q) đi qua điểm $\Large A(-2; -1; 5)$.