Cho hàm số $\Large f(x)$ có đồ thị $\Large y={f}'(x)$ như hình dưới đâ

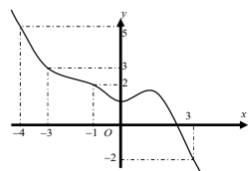
Cho hàm số $\Large f(x)$ có đồ thị $\Large y={f}'(x)$ như hình dưới đây. Trên [-4; 3] hàm số $\Large g(x)=2f(x)+(1-x)^2$ đạt giá trị nhỏ nhất tại điểm nào trong các điểm sau đây?

• A.

  $\Large x_0=-4$.

• B.

  $\Large x_0=-1$.

• C.

  $\Large x_0=3$.

• D.

  $\Large x_0=-3$.

Chọn B

Ta có $\Large g(x)=2f(x)+(1-x)^2$ suy ra $\Large {g}'(x)=2{f}'(x)-2(1-x)=2\big[{f}'(x)-(1-x)\big]$.

Xét $\Large y={f}'(x)$ có đồ thị như hình vẽ, $\Large y=1-x$ là đường thẳng đi qua các điểm (3; -2), (-1; 2), (-4; 5).

Đồ thị hàm số $\Large y={f}'(x)$ cắt đường thẳng $\Large y=1-x$ tại các điểm $\Large x=-4, x=-1, x=3$.

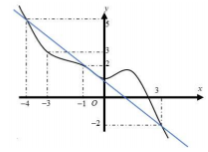
Lập bảng biến thiên của $\Large {g}'(x)={f}'(x)-(1-x)$ trong đoạn [-4; 3] ta có

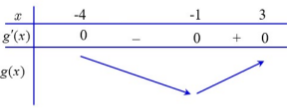
Từ bảng biến thiên, hàm số $\Large g(x)=2f(x)+(1-x)^2$ đạt giá trị nhỏ nhất tại điểm $\Large x_0=-1$.