Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt

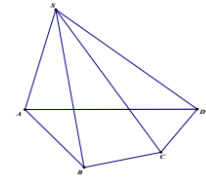
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng (SAB), (SBC), (SCD), (SDA) với mặt đáy lần lượt là $\Large 90^{\circ}, 60^{\circ}, 60^{\circ}, 60^{\circ}$. Biết rằng tam giác SAB vuông cân tại S, $\Large AB=a$ và chu vi tứ giác ABCD là $\Large 9a$. Tính thể tích V của khối chóp S.ABCD

• A.

  $\Large V=\dfrac{a^3\sqrt{3}}{4}$.

• B.

  $\Large V=a^3\sqrt{3}$.

• C.

  $\Large V=\dfrac{2a^3\sqrt{3}}{9}$.

• D.

  $\Large V=\dfrac{a^3\sqrt{3}}{9}$.

Chọn D

Gọi H là trung điểm đoạn thẳng AB, khi đó $\Large SH\perp (ABCD)$.

Lần lượt vẽ HI, HJ, HK vuông góc với BC, CD, DA tại I, J, K.

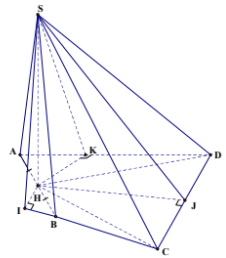
Khi đó $\Large \big[\widehat{(SBC); (ABCD)}\big]=\widehat{(SI; IH)}=\widehat{SIH}, \big[\widehat{(SCD), (ABCD)}\big]=\widehat{(SJ, JH)}=\widehat{SJH}$ và $\Large \big[\widehat{(SDA), (ABCD)}\big]=\widehat{(SK, KH)}=\widehat{SKH} \Rightarrow \widehat{SIH}=\widehat{SJH}=\widehat{SKH}=60^{\circ}$.

Ta có $\Large AB+BC+CD+DA=9a \Rightarrow BC+CD+DA=9a-AB=8a$.

Thể tích khối chóp S.ABCD là $\Large V_{S.ABCD}=\dfrac{1}{3}SH.S_{ABCD}$.

Lại có $\Large S_{ABCD}=S_{HBC}+S_{HCD}+S_{HAD}=\dfrac{1}{2}HI.BC+\dfrac{1}{2}HJ.CD+\dfrac{1}{2}HK.DA$.

Mặt khác $\Large HI=HJ=HK=\dfrac{SH}{\tan60^{\circ}}=\dfrac{AB}{2\sqrt{3}}=\dfrac{a}{2\sqrt{3}}$.

Do đó $\Large S_{ABCD}=\dfrac{1}{2}.\dfrac{a}{2\sqrt{3}}.(BC+CD+DA)=\dfrac{1}{2}.\dfrac{a}{2\sqrt{3}}.8a=\dfrac{2a^2\sqrt{3}}{3}$.

Vậy $\Large V_{ABCD}=\dfrac{1}{3}.\dfrac{a}{2}.\dfrac{2a^2\sqrt{3}}{3}=\dfrac{a^3\sqrt{3}}{9}$.