Cho hàm số $\Large y=x^3-3mx^2+3(m^2-1)x-m^3$ với m là tham số. Gọi (C

Cho hàm số $\Large y=x^3-3mx^2+3(m^2-1)x-m^3$ với m là tham số. Gọi (C) là đồ thị của hàm số đã cho. Biết rằng khi m thay đổi, điểm cực tiểu của đồ thị (C) luôn nằm trên một đường thẳng d cố định. Tìm hệ số góc k của đường thẳng d.

• A.

  $\Large k=-\dfrac{1}{3}$.

• B.

  $\Large k=3$.

• C.

  $\Large k=\dfrac{1}{3}$.

• D.

  $\Large k=-3$.

Chọn D

Ta có: $\Large {y}'=3x^2-6mx+3m^2-3=0 \Rightarrow \Leftrightarrow x^2-2mx+m^2=1 \Leftrightarrow (x-m)^2=1$ $\Large \Leftrightarrow \left[\begin{align} & x=m-1 \\ & x=m+1 \end{align}\right.$.

Bảng xét dấu $\Large {y}'$:

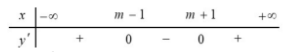
Suy ra điểm cực tiểu của hàm số: $\Large x_{CT}=m+1$.

Ta có:

$\Large y=x^3-3mx^2+3(m^2-1)x-m^3=(x-m)^3-3x \Rightarrow y(m+1)=1-3(m+1) \Rightarrow y_{CT}=-3x_{CT}+1$

$\Large \Rightarrow$ điểm cực tiểu của đồ thị (C) luôn nằm trên đường thẳng $\Large d: y=-3x+1$ suy ra $\Large k=-3$.