Cho hình chóp S.ABC có mặt đáy là tam giác đều cạnh bằng 2 và hình chi

Cho hình chóp S.ABC có mặt đáy là tam giác đều cạnh bằng 2 và hình chiếu của S lên mặt phẳng (ABC) là điểm H nằm trong tam giác ABC sao cho $\Large \widehat{AHB}=150^{\circ}; \widehat{BHC}=120^{\circ}; \widehat{CHA}=90^{\circ}$. Biết tổng diện tích mặt cầu ngoại tiếp các hình chóp S.HAB; S.HBC; S.HCA là $\Large \dfrac{124}{3}\pi$. Tính thể tích khối chóp S.ABC.

• A.

  $\Large V_{S.ABC}=\dfrac{9}{2}$.

• B.

  $\Large V_{S.ABC}=\dfrac{4}{3}$.

• C.

  $\Large V_{S.ABC}=4$.

• D.

  $\Large V_{S.ABC}=\dfrac{8}{3}$.

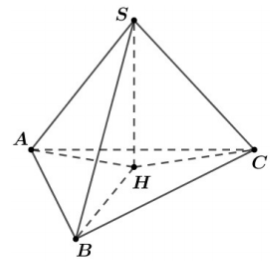
Gọi $\Large R_1, R_2, R_3$ là bán kính mặt cầu ngoại tiếp hình chóp S.HAB, S.HBC, S.HCA.

Gọi $\Large r_1, r_2, r_3$ là bán kính đường tròn ngoại tiếp HAB, HBC, HCA.

Tổng diện tích mặt cầu ngoại tiếp $\Large 4\pi (R_1^2+R_2^2+R_3^2)=\dfrac{124}{3}\pi$

$\Large \Leftrightarrow \left(r_1^2+\dfrac{h^2}{4}\right)+\left(r_2^2+\dfrac{h^2}{4}\right)+\left(r_3^2+\dfrac{h^2}{4}\right)=\dfrac{31}{3}$

$\Large \Leftrightarrow \dfrac{3}{4}h^2+\left(\dfrac{2}{2\sin90^{\circ}}\right)^2+\left(\dfrac{2}{2\sin120^{\circ}}\right)^2+\left(\dfrac{2}{2\sin150^{\circ}}\right)^2=\dfrac{31}{3} \Leftrightarrow h=\dfrac{4}{\sqrt{3}}$

Do đó thể tích khối chóp $\Large V=\dfrac{1}{3}.S_{ABC}.h=\dfrac{1}{3}.\dfrac{4\sqrt{3}}{4}.\dfrac{4}{\sqrt{3}}=\dfrac{4}{3}$.