Cho hình chóp $\Large S.ABC$ có đáy là tam giác đều cạnh a. Hình chiếu

Cho hình chóp $\Large S.ABC$ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABC) là điểm H trên cạnh AB sao cho $\Large HA=2HB$. Góc giữa SC và mặt phẳng (ABC) bằng $\Large 60^{\circ}$. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.

• A.

  $\Large \dfrac{a\sqrt{42}}{8}$.

• B.

  $\Large \dfrac{a\sqrt{42}}{3}$.

• C.

  $\Large \dfrac{a\sqrt{6}}{8}$.

• D.

  $\Large \dfrac{a\sqrt{6}}{7}$.

Chọn A

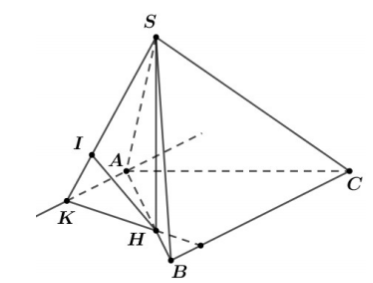
Vì $\Large SH\perp (ABC)$ nên góc giữa SC và (ABC) là $\Large \widehat{SCH}=60^{\circ}$.

Từ A kẻ đường thẳng Ax song song với BC. Từ H kẻ $\Large HK\perp Ax$ tại K, kẻ $\Large HI\perp SK$ tại I.
Khi đó $\Large BC // (SAx)$ nên $\Large d(BC, SA)=d\big(BC, (SAx)\big)=d\big(B, (SAx)\big)=\dfrac{3}{2}d\big(H, (SAx)\big)=\dfrac{3}{2}HI$.

Xét tam giác SHK vuông tại H có

$\Large SH=HC.\tan 60^{\circ}=\sqrt{BC^2+BH^2-2BC.BH.\cos 60^{\circ}}.\tan 60^{\circ}=\dfrac{\sqrt{7}}{3}.\sqrt{3}=\dfrac{\sqrt{21}}{3}$.

$\Large HK=\dfrac{2}{3}d(A, BC)=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}$.

Do đó $\Large HI=\dfrac{SH.HK}{\sqrt{SH^2+HK^2}}=\dfrac{\sqrt{42}a}{12}$.

Vậy $\Large d(BC, SA)=\dfrac{3}{2}.\dfrac{\sqrt{42}a}{12}=\dfrac{a\sqrt{42}}{8}$.