Trong không gian, cho tam giác $\Large ABC$ vuông cân tại $\Large A$,

Trong không gian, cho tam giác $\Large ABC$ vuông cân tại $\Large A$, $\Large BC = 2a$. Khi quay tam giác $\Large ABC$ quanh cạnh góc vuông $\Large AC$ thì đường gấp khúc $\Large ABC$ tạo thành một hình nón. Diện tích xung quanh của hình nón đó bằng

• A.

  A. $\Large 4 \pi a^{2}$

• B.

  B. $\Large 2 \pi a^{2} \sqrt{2}$

• C.

  C. $\Large 2 \pi a^{2}$

• D.

  D. $\Large 4 \pi a^{2} \sqrt{2}$

Chọn B

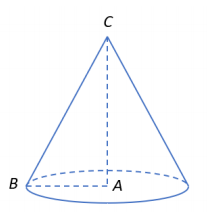
Tam giác $\Large ABC$ vuông cân tại $\Large A$ nên:

$\Large BC^{2} = AB^{2} + AC^{2}$

=> $\Large 2.AB^{2} = BC^{2} = 4a^{2}$

=> $\Large AB = a \sqrt{2}$

Khi quay tam giác $\Large ABC$ xung quanh cạnh góc vuông $\Large AC$ thì đường gấp khúc $\Large ABC$ tạo thành một hình nón có độ dài đường sinh $\Large l = BC = 2a$, bán kính đáy $\Large r = AB = a \sqrt{2}$.

Diện tích xung quanh hình nón đó là:

$\Large S_{xq} = \pi . a \sqrt{2} . 2a = 2 \pi a^{2} \sqrt{2}$.