Trong cac số phức z thỏa mãn $\Large |z-3-4 i|=2$ có hai số phức $\Lar

MỤC LỤC
Câu hỏi:
Trong cac số phức z thỏa mãn $\Large |z-3-4 i|=2$ có hai số phức $\Large z_{1}, z_{2}$ thỏa mãn $\Large \left|z_{1}-z_{2}\right|=1$. Giá trị nhỏ nhất của $\Large \left|z_{1}\right|^{2}-\left|z_{2}\right|^{2}$ bằng
Đáp án án đúng là: A
Lời giải chi tiết:
Đặt $\Large \left\{\begin{array}{l}
z_{1}=a+b i \\
z_{2}=c+d i
\end{array}(a, b, c, d \in R )\right.$. Theo đề ta có: $\Large \left\{\begin{array}{l}
(a-3)^{2}+(b-4)^{2}=4(1) \\
(c-3)^{2}+(d-4)^{2}=4(2) \\
(a-c)^{2}+(b-d)^{2}=1(3)
\end{array}\right.$
Khi lấy 910 -(2) theo vế ta có $\Large a^{2}+b^{2}-c^{2}-d^{2}=6(a-c)+8(b-d)$
Kết hợp sử dụng bất đằng thức Cauchy-Schwarz và sử dụng (3) ta có:
$\Large \left|z_{1}\right|^{2}-\left|z_{2}\right|^{2}=a^{2}+b^{2}-c^{2}-d^{2}=6(a-c)+8(b-d) \geq-\sqrt{\left(6^{2}+8^{2}\right)\left[(a-c)^{2}+(b-d)^{2}\right]}=-10$
vậy giá trị nhỏ nhát của $\Large \left|z_{1}\right|^{2}-\left|z_{2}\right|^{2}$ là -10 khi $\Large \left\{\begin{array}{l}
(a-3)^{2}+(b-4)^{2}=4 \\
(c-3)^{2}+(d-4)^{2}=4 \\
(a-c)^{2}+(b-d)^{2}=1 \\
\dfrac{a-c}{6}=\dfrac{b-d}{8}=k<0
\end{array}\right.$
Tồn tại 2 cặp số phức thỏa mãn là: 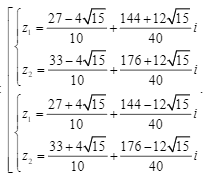
Xem thêm các bài tiếp theo bên dưới
- Gọi S là tập hợp các số phức thỏa $\Large |z-3|+|z+3|=10$. Gọi $\Large
- Cho số phức z thỏa mãn điều kiện $\Large |z+2-i|-|z-2-3 i|=2 \sqrt{5}$
- Cho số thực $\Large z_{1}$ và số phức $\Large z_{2}$ thỏa mãn $\Large
- Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\large (P):\,
- Cho a, b, c là các số thực dương, khác 1 và thỏa mãn $\large \log_ab^2