Tính tổng T tất cả giá trị của tham số m để phương trình $\Large 2^{(x

Tính tổng T tất cả giá trị của tham số m để phương trình $\Large 2^{(x-1)^2}\log_{2}(x^2-2x+3)=4^{\left|x-m\right|}\log_{2}{(2\left|x-m\right|+2)}$ có đúng ba nghiệm phân biệt 

• A.

  A. T = 1

• B.

  B. T = 2

• C.

  C. T = 3

• D.

  D. T = 4

Chọn C

Phương trình trở thành $\Large 2^{(x-1)^2}.\log_{2}\left[(x-1)^2+2\right]=2^{2\left|x-m\right|}.\log_{2}(2\left|x-m\right|+2)$ (1)

Xét hàm số $\Large f(t)=2^t.\log_{2}(t+2), t\geq0\Rightarrow f'(t)=2^t.\log_{2}(t+2)\ln2+\dfrac{2^t}{(t+2)\ln2}>0, t\geq0$

$\Large \Rightarrow$ hàm số đồng biến trên $\Large [0; +\infty)$

Do đó: $\Large (1)\Leftrightarrow f\left[(x-1)^2\right]=f(2\left|x-m\right|)\Leftrightarrow (x-1)^2=2\left|x-m\right|$ $\Large \Leftrightarrow \left[\begin{align}&m=-\dfrac{x^2}{2}+2x-\dfrac{1}{2}\\&m=\dfrac{x^2+1}{2}\\\end{align}\right.$ (*)

Số nghiệm pt (*) là số giao điểm của đường thẳng $\Large y =m$ và đồ thị hàm số $\Large y=\left\{\begin{align}&-\dfrac{x^2}{2}+2x-\dfrac{1}{2}\\&\dfrac{x^2+1}{2}\\\end{align}\right.$

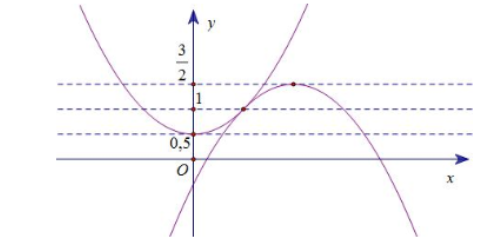
Dựa vào đồ thị hàm số (*) có 3 nghiệm phân biệt $\Large \Rightarrow m=\dfrac{1}{2}; m=1; m=\dfrac{3}{2}$