Tìm tất cả các giá trị của tham số $\Large m$ để phương trình $\Large

Tìm tất cả các giá trị của tham số $\Large m$ để phương trình $\Large 9.9^{x^2-2x}-(2m+1)15^{x^2-2x+1}+(4m-2).5^{2x^2-4x+2}=0$ có 2 nghiệm thực phân biệt.

 

• A.

  A. $\Large \dfrac{1}{2} < m < 1$

   
• B.

  B. $\Large m>\dfrac{3-\sqrt{6}}{2}$ hoặc $\Large m < \dfrac{3-\sqrt{6}}{2}$

   
• C.

  C. $\Large m>1$ hoặc $\Large m < \dfrac{1}{2}$

   
• D.

  D. $\Large \dfrac{3-\sqrt{6}}{2} < m < \dfrac{3+\sqrt{6}}{2}$

Chọn A

Ta có: 

$\Large 9.9^{x^2-2x}-(2m+1).15^{x^2-2x+1}+(4m-2).5^{2x^2-4x+2}=0$

$\Large \Leftrightarrow 9^{x^2-2x+1}-(2m+1).15^{x^2-2x+1}+(4m-2).25^{x^2-2x+1}=0 $ 

$\Large \Leftrightarrow \left[\left(\dfrac{3}{5}\right)^{(x-1)^2}\right]^2-(2m+1)\left(\dfrac{3}{5}\right)^{(x-1)^2}+4m-2=0$ (1)

Đặt $\Large \left(\dfrac{3}{5}\right)^{(x-1)^2}=t>0$

Khi đó (1) trở thành 

$\Large t^2-(2m+1)t+4m-2=0\Leftrightarrow (t-2)(t-2m+1)=0$ $\Large \Leftrightarrow\left[\begin{align}&t=2\\&t=2m-1\\\end{align}\right.$

Chú ý rằng với $\Large t=2\Leftrightarrow \left(\dfrac{3}{5}\right)^{(x-1)^2}=2\Leftrightarrow (x-1)^2=\log_{\dfrac{3}{5}}2$ mà $\Large \log_{\dfrac{3}{5}}2<0$ và $\Large (x-1)^2\geq 0$ nên phương trình này vô nghiệm

Do đó: $\Large (1)\Leftrightarrow \left(\dfrac{3}{5}\right)^{(x-1)^2}=2m-1$ (2)

Xét hàm số $\Large f(x)=\left(\dfrac{3}{5}\right)^{(x-1)^2}$ có $\Large f'(x)=\left(\dfrac{3}{5}\right)^{(x-1)^2}.\ln\left(\dfrac{3}{5}\right).2(x-1); f'(x)=0\Leftrightarrow x=1$

Bảng biến biên hàm số $\Large f(x)$

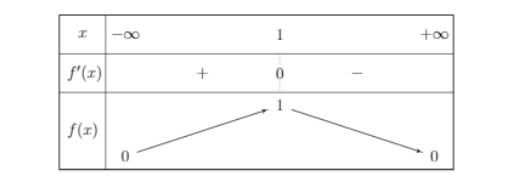
Dựa vào bảng biến thiên, số nghiệm của phương trình là số giao điểm của đồ thị hàm số $\Large y=f(x)$ và đường thẳng $\Large y=2m-1$ nên điều kiện của $\Large m$ thỏa mãn là $\Large 0<2m-1<1\Leftrightarrow \dfrac{1}{2}