Gọi $\Large a$ là số thực lớn nhất để bất phương trình $\Large x^2-x+2

Gọi $\Large a$ là số thực lớn nhất để bất phương trình $\Large x^2-x+2+a\ln (x^2-x+1)\geq 0$ nghiệm đúng với mọi $\Large x\in\mathbb{R}$. Mệnh đề nào sau đây đúng?

 

• A.

  A. $\Large a\in(2; 3]$

   
• B.

  B. $\Large a\in (8; +\infty)$

   
• C.

  C. $\Large a\in (6; 7]$

   
• D.

  D. $\Large a\in (-6; -5]$

Chọn C

Đặt: $\Large t=x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}$ suy ra $\Large t\geq\dfrac{3}{4}$

Bất phương trình đã cho trở thành: 

$\Large x^2-x+2+a\ln(x^2-x+1)\geq 0\Leftrightarrow t+a\ln t+1\geq 0\Leftrightarrow  a\ln t\geq -t-1$

- Trường hợp 1: t = 1 khi đó: $\Large a\ln 1\geq -1-1$ luôn đúng với mọi $\Large a$

- Trường hợp 2: $\Large \dfrac{3}{4}\leq t<1$

   Ta có: $\Large a\ln t\geq -t-1, \forall t\in\left[\dfrac{3}{4}; 1\right)\Leftrightarrow a\leq \dfrac{-t-1}{\ln t}, \forall t\in\left[\dfrac{3}{4}; 1\right)$

   Xét hàm số $\Large f(t)=\dfrac{-t-1}{\ln t}\Rightarrow f'(t)=-\dfrac{\ln t-1-\dfrac{1}{t}}{\ln^2 t}\geq 0, \forall t\in\left[\dfrac{3}{4}; 1\right)$

   Do đó: $\Large a\leq \dfrac{-t-1}{\ln t}, \forall t\in\left[\dfrac{3}{4}; 1\right)\Leftrightarrow a\leq \min f(t)=\dfrac{-7}{4\ln\dfrac{3}{4}}$

- Trường hợp 3: $\Large t > 1$

   Ta có: $\Large a\ln t\geq -t-1, \forall t\in (1; +\infty)\Leftrightarrow  a\geq \dfrac{-t-1}{\ln t}, \forall t\in (1; +\infty)$

   Xét hàm số: $\Large f(t)=\dfrac{-t-1}{\ln t}\Rightarrow f'(t)=-\dfrac{\ln t-1-\dfrac{1}{t}}{\ln^2 t}, \forall t\in (1; +\infty)$

   Xét hàm số: $\Large g(t)=\ln t-1-\dfrac{1}{t}\Leftrightarrow g'(t)=\dfrac{1}{t}+\dfrac{1}{t^2}>0$ nên hàm số đồng biến

   Suy ra phương trình $\Large g(t)=0$ có tối đa một nghiệm 

   Vì $\Large g(1)=-2; \underset{t\rightarrow +\infty}{lim} g(t)=+\infty$ nên $\Large g(t)=0$ có duy nhất một nghiệm trên $\Large (1; +\infty)$

Do đó: $\Large f'(t)=0$ có duy nhất một nghiệm là $\Large t_{0}$. Khi đó: $\Large \ln t_{0}=\dfrac{t_{0}+1}{t_{0}}$ suy ra $\Large f(t_{0})=-t_{0}$. Bảng biến thiên:

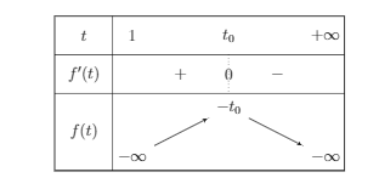
Suy ra: $\Large a\geq \dfrac{-t-1}{\ln t}, \forall t\in (1; +\infty) \Leftrightarrow a\geq -t_{0}>1$

Kết hợp 3 TH ta có: $1<\Large -t_{0}\leq a\leq\dfrac{-7}{4\ln\dfrac{3}{4}}\approx 6, 08$

Vậy số thực $\Large a$ thỏa mãn yêu cầu bài toán là: $\Large a\in (6; 7]$