Tìm giá trị nhỏ nhất của hàm số $\large y=-x+3-\dfrac{1}{x+2}$ trên nử

Tìm giá trị nhỏ nhất của hàm số $\large y=-x+3-\dfrac{1}{x+2}$ trên nửa khoảng [-4;-2).

• A.

  A. $\large \min _{[-4,-2)}=5$

• B.

  B. $\large \min _{[-4,-2)}=6$

• C.

  C. $\large \min _{[-4,-2)}=4$

• D.

  D. $\large \min _{[-4,-2)}=7$

Chọn D

Xét hàm số $\large y=-x+3-\dfrac{1}{x+2}$ trên nửa khoảng [-4;-2)

$\large y^{\prime}=-1+\dfrac{1}{(x+2)^{2}}=\dfrac{-x^{2}-4 x-3}{(x+2)^{2}}$

$\large y^{\prime}=0 \Leftrightarrow-x^{2}-4 x-3=0 \Leftrightarrow\left[\begin{array}{l}
x=-1 \notin[-4 ;-2) \\
x=-3 \in[-4 ;-2)
\end{array}\right.$

Bảng biến thiên

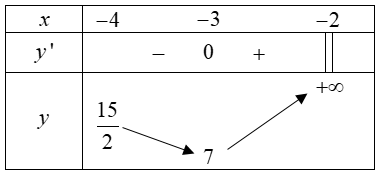
Dựa vào bảng biến thiên vậy $\large \min _{[-4;-2)} y=7$.