Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh

Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng $\Large a\sqrt{2}.$ Một thiết diện qua đỉnh tạo với đáy một góc $\Large 60^{\circ}.$ Diện tích của thiết diện này bằng

• A.

  A. $\Large \dfrac{a^2\sqrt{2}}{3}.$

• B.

  B. $\Large \dfrac{a^2\sqrt{2}}{2}.$

• C.

  C. $\Large 2a^2.$

• D.

  D. $\Large \dfrac{a^2\sqrt{2}}{4}.$

Chọn A

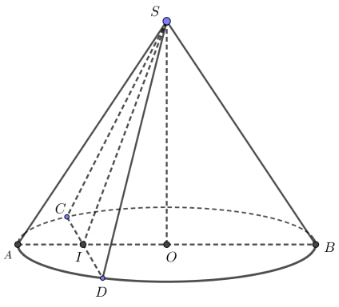
Giả sử hình nón có đỉnh $\Large S$, tâm đường tròn đáy là $\Large O.$

Thiết diện qua trục là $\Large \Delta SAB,$ thiết diện qua đỉnh là $\Large \Delta SCD$

Gọi $\Large I$ là trung điểm của $\Large CD.$

Theo giả thiết ta có $\Large \Delta SAB$ vuông cân tại S, cạnh huyền $\Large AB=a\sqrt{2}$ $\Large \Rightarrow r=OA=\dfrac{a\sqrt{2}}{2}$

$\Large SA=SB=l=a$

$\Large \Rightarrow h=SO$ $\Large =\sqrt{SA^2-OA^2}$ $\Large =\sqrt{a^2-\dfrac{2a^2}{4}}$ $\Large =\dfrac{a\sqrt{2}}{2}.$

Ta lại có $\Large \widehat{SIO}=60^{\circ}$ $\Large \Rightarrow \sin{60}^{\circ}=\dfrac{SO}{SI}$ $\Large \Rightarrow SI=\dfrac{SO}{\sin{60}^{\circ}}=\dfrac{\dfrac{a\sqrt{2}}{2}}{\dfrac{\sqrt{3}}{2}}=\dfrac{a\sqrt{6}}{3}.$

$\Large ID=\sqrt{SD^2-SI^2}$ $\Large =\sqrt{a^2-\dfrac{6a^2}{9}}$ $\Large =\dfrac{a\sqrt{3}}{3}$ $\Large \Rightarrow CD=\dfrac{2a\sqrt{3}}{3}.$

Diện tích thiết diện cần tìm là $\Large S_{\Delta SCD}=\dfrac{1}{2}.\dfrac{2a\sqrt{3}}{3}.\dfrac{a\sqrt{6}}{3}=\dfrac{a^2\sqrt{2}}{3}.$