Một vật nhỏ có khối lượng 500 g dao động điều hòa trên trục Ox, đồ thị

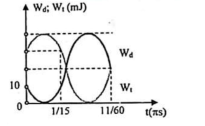
Một vật nhỏ có khối lượng 500 g dao động điều hòa trên trục Ox, đồ thị động năng và thế năng của vật theo thời gian như hình vẽ. Sau bao lâu kể từ lúc bắt đầu chuyển động, vật đổi chiều lần thứ hai?

• A.

  $\Large \dfrac{7\pi}{15}s.$

• B.

  $\Large \dfrac{14\pi}{30}s.$

• C.

  $\Large \dfrac{7\pi}{30}s.$

• D.

  $\Large \dfrac{4\pi}{15}s.$

Phương pháp: 
Sử dụng kĩ năng đọc đồ thị 
Mối liên hệ giữa thế năng và li độ: $\Large W_t=nW \Rightarrow x=\pm A\sqrt{n}$
Sử dụng vòng tròn lượng giác và công thức: $\Large \omega=\dfrac{\Delta \varphi}{\Delta t}$
Cách giải: 
Từ đồ thị ta thấy ở thời điểm $\Large t_1=\dfrac{\pi}{15}s$ và $\Large t_2=\dfrac{11\pi}{60}s$ thế năng của vật lần lượt là: 

$\Large \left\{\begin{align} & W_{t1}=\dfrac{3}{4}W \Rightarrow x_1=\dfrac{\pm A\sqrt{3}}{2} \\ & W_{t2}=\dfrac{1}{2}W \Rightarrow x_2=\dfrac{\pm A}{\sqrt{2}} \end{align}\right.$
Từ đồ thị ta có vòng tròn lượng giác: 

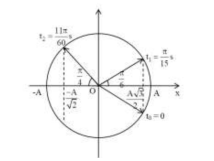
Từ vòng tròn lượng giác, ta thấy từ thời điểm $\Large t_1$ đến thời điểm $\Large t_2,$ vecto quay được góc: 
$\Large \Delta \varphi=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{4}=\dfrac{7\pi}{12} (rad)$
Ta có: $\Large \omega =\dfrac{\Delta \varphi}{\Delta t}=\dfrac{\dfrac{7\pi}{12}}{\dfrac{11\pi}{60}-\dfrac{\pi}{15}}=5 (rad/s)$
Từ thời điểm $\Large t_0$ đến khi vật đổi chiều lần thứ 2, vật tới li độ $\Large x = -A$ lần đầu tiên, vecto quay được góc là: 
$\Large \Delta {\varphi}'=\dfrac{\pi}{6}+\pi=\dfrac{7\pi}{6} (rad) \Rightarrow \Delta{t}'=\dfrac{\Delta {\varphi}'}{\omega}=\dfrac{\dfrac{7\pi}{6}}{5}=\dfrac{7\pi}{30}(s)$
Chọn C.