Hai nguồn sóng kết hợp O1,O2 cách nhau 25 cm, dao động cùn

MỤC LỤC
Câu hỏi:
Hai nguồn sóng kết hợp O1,O2 cách nhau 25 cm, dao động cùng pha. Ở mặt chất lỏng, điểm M cách O1,O2 lần lượt là 15 cm và 20 cm dao động với biên độ cực đại. Số điểm dao động với biên độ cực đại trên MO2 nhiều hơn so với trên MO1 là 8. Xét các điểm trên mặt chất lỏng thuộc đường thẳng vuông góc với O1O2 tại O1, điểm dao động với biên độ cực đại cách M một đoạn nhỏ nhất là
Đáp án án đúng là: A
Lời giải chi tiết:
Phương pháp:
Số cực đại giao thoa: N=2m+1
Điều kiện cực đại: d2−d1=kλ
Cách giải:
Gọi số cực đại trên MO1 là m → số cực đại trên MO2 là m + 8
Tổng số cực đại giao thoa là: N=m+m+8+1=2m+9 (tính cả đường trung trực)
Vậy trên mỗi nửa đoạn O1O2 có m + 4 cực đại → tại m là cực đại bậc 4
Ta có: MO2−MO1=kλ⇒20−15=4λ⇒λ=1,25(cm)
Số cực đại trên mỗi nửa đoạn O1O2 là: N=[O1O2λ]=[251,25]=20
Ta có hình vẽ:
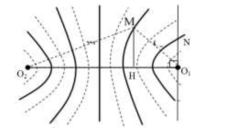
Đặt MH=x, ta có:
O1O2=O1H+O2H⇒O1O2=√MO22−x2+√MO21−x2
⇒25=√202−x2+√152−x2⇒x=12(cm)⇒O1H=9(cm)
Để N gần M nhất, khoảng cách O1N gần với x nhất
Gọi N là cực đại bậc k, O1N=y, ta có:
NO2−NO1=kλ⇒√y2+252−y=k.1,25
Với y=12cm⇒k=12,57⇒k=13
⇒√y2+252−y=13.1,25⇒y≈11,1(cm)
MN=√O1H2+(MH−O1N)2=9,045(cm)=90,45(mm)
Chọn A.
Xem thêm các bài tiếp theo bên dưới
- Từ một trạm điện, điện năng được truyền tải đến nơi tiêu thụ bằng đườn
- Một chất điểm tham gia đồng thời hai dao động điều hòa, cùng phương, c
- Một nguồn sáng điểm A thuộc trục chính của một thấu kính mỏng, cách qu
- Sóng vô tuyến truyền thẳng trong không gian là sóng ngắn. sóng dài. só
- Biết rằng điểm biểu diễn số phức z là điểm M ở hình bên. Mô đun của z