Một vật có khối lượng 250 g dao động điều hòa, chọn gốc tính thế năng

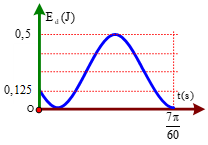
Một vật có khối lượng 250 g dao động điều hòa, chọn gốc tính thế năng ở vị trí cân bằng, đồ thị động năng theo thời gian như hình vẽ. Thời điểm đầu tiên vật có vận tốc thỏa mãn v = 10x (x là li độ) là:

• A.

   A. $\Large \dfrac{7\pi }{12} s$

• B.

  B. $\Large \dfrac{11\pi }{120} s$

• C.

  C. $\Large \dfrac{\pi }{20} s$

• D.

  D. $\Large \dfrac{\pi }{24} s$

+ Từ đồ thị, ta thấy thời điểm t = 0 vật có thế năng bằng 3 lần động năng $\Large \Rightarrow x=\pm \dfrac{\sqrt{3}A}{2}$ , động năng giảm đến cực tiểu tăng đến cực đại rồi giảm về cực tiểu tương ứng: $\Large \Delta t=\dfrac{T}{12}+\dfrac{T}{2}=\dfrac{7\pi }{60}\Rightarrow T=0,2\pi s\Rightarrow \omega =10\left( rad/s \right)$

+ Ta có: $\Large{{\left( \dfrac{x}{A} \right)}^{2}}+{{\left( \dfrac{v}{\omega A} \right)}^{2}}=1;v=10x\Rightarrow x=\pm \dfrac{\sqrt{2}}{2}A$

→ Thời điểm gần nhất ứng với: $\Large \Delta t=\dfrac{T}{12}+\dfrac{T}{8}+\dfrac{T}{4}=\dfrac{11\pi }{120}s$ do v ,x cùng dấu => v < 0, x < 0