Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, gốc O ở VT
MỤC LỤC
Câu hỏi:
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, gốc O ở VTCB. Tại các thời điểm $t_{1}; t_{2}; t_{3}$ lò xo dãn a (cm); 2a (cm); 3a (cm) tương ứng với tốc độ của vật là $\Large v\sqrt{8}\left( cm/s \right);v\sqrt{6}\left( cm/s \right)$ và $\Large v\sqrt{2}\left( cm/s \right)$.Tỉ số giữa thời gian lò xo nén và lò xo dãn trong 1 chu kỳ là
Đáp án án đúng là: B
Lời giải chi tiết:
|
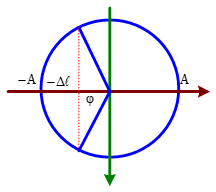
+ Giả sử ở VTCB lò xo dãn Δℓ + Áp dụng hệ thức độc lâp: $\Large{{A}^{2}}={{\left( a-\Delta \ell \right)}^{2}}+\dfrac{8{{v}^{2}}}{{{\omega }^{2}}}$ $\Large{{A}^{2}}={{\left( 2a-\Delta \ell \right)}^{2}}+\dfrac{6{{v}^{2}}}{{{\omega }^{2}}};{{A}^{2}}={{\left( 3a-\Delta \ell \right)}^{2}}+\dfrac{2{{v}^{2}}}{{{\omega }^{2}}}$ + Từ 3 phương trình trên ta được $\Large a=2\Delta \ell \Rightarrow A=\sqrt{33}\Delta \ell $ + Biểu diễn vị trí lò xo nén $\Large \left( -\Delta \ell ;-A \right)$ và lò xo dãn $\Large \left( -\Delta \ell ;A \right)$ |
|
$\Large \cos \varphi =\dfrac{\Delta \ell }{A}=\dfrac{1}{\sqrt{33}}\Rightarrow \varphi ={{80}^{0}}$
+ Tỉ số lò xo nén và dãn trong 1 chu kỳ là: $\Large \dfrac{{{t}_{nen}}}{{{t}_{dan}}}=\dfrac{160}{200}=0,8$
Xem thêm các bài tiếp theo bên dưới
- Một con lắc lò xo có m = 100 g và k = 12,5 N/m. Thời điểm ban đầu (t =
- Có hai con lắc đơn giống nhau. Vật nhỏ của con lắc thứ nhất mang điện
- Hai điểm sáng dao động điều hòa trên cùng một trục Ox quanh vị trí cân
- Một vật có khối lượng không đổi thực hiện đồng thời hai dao động điều
- Hai con lắc lò xo hoàn toàn giống nhau, gồm lò xo nhẹ độ cứng 10 N/m v