Hai con lắc lò xo hoàn toàn giống nhau, gồm lò xo nhẹ độ cứng 10 N/m v

Hai con lắc lò xo hoàn toàn giống nhau, gồm lò xo nhẹ độ cứng 10 N/m và vật nhỏ khối lượng 250 g. Treo các con lắc thẳng đứng tại nơi có g = 10 m/s², điểm treo của chúng ở cùng độ cao và cách nhau 5 cm. Kéo vật nhỏ của con lắc thứ nhất xuống dưới vị trí cân bằng của nó 7 cm, con lắc thứ hai được kéo xuống dưới vị trí cân bằng của nó 5 cm. Thời điểm ban đầu thả nhẹ con lắc thứ nhất, đến thời điểm t = $\Large \dfrac{1}{6}$ s thả nhẹ con lắc thứ hai,các con lắc dao động điều hòa theo phương thẳng đứng. Lấy π² = 10. Khoảng cách lớn nhất giữa hai vật nhỏ của hai con lắc là

• A.

  A. 8,6 cm.

• B.

  B. 8,0 cm.

• C.

  C. 7,8 cm.

• D.

  D. 6,0 cm.

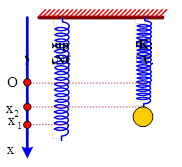
+ Tần số góc dao động của hai con lắc:

$\Large \omega =\sqrt{\dfrac{k}{m}}=2\pi \left( rad/s \right)\Rightarrow T=1\left( s \right)$

+ Chọn hệ trục tọa độ có phương thẳng đứng, chiều dương hướng xuống, gốc tọa độ tại VTCB chung của hai con lắc lò xo

+ Chọn gốc thời gian là lúc bắt đầu thả  nhẹ con lắc thứ hai, khi đó phương trình dao động của hai con lắc sẽ là:

$\Large {{x}_{1}}=7\cos \left( 2\pi t+\dfrac{\pi }{3} \right)cm;{{x}_{2}}=5\cos \left( 2\pi t \right)cm$

$\Rightarrow \Delta {{x}_{\max }}=\sqrt{{{7}^{2}}+{{5}^{2}}-2.5.7.\cos \left( \dfrac{\pi }{3} \right)}=\sqrt{39}\left( cm \right)$

→ Khoảng cách lớn nhất giữa hai vật: $\Large{{d}_{\max }}=\sqrt{{{5}^{2}}+\Delta x_{\max }^{2}}=8\left( cm \right)$