Một con lắc lò xo có m = 100 g và k = 12,5 N/m. Thời điểm ban đầu (t =

Một con lắc lò xo có m = 100 g và k = 12,5 N/m. Thời điểm ban đầu (t =

Bài sau

4/5

Tác giả: Thầy Tùng

Đăng ngày: 18 Aug 2022

Lưu về Facebook:
Hình minh họa Một con lắc lò xo có m = 100 g và k = 12,5 N/m. Thời điểm ban đầu (t =

MỤC LỤC

Câu hỏi:

Một con lắc lò xo có m = 100 g và k = 12,5 N/m. Thời điểm ban đầu (t = 0), lò xo không biến dạng, thả nhẹ để hệ vật và lò xo rơi tự do sao cho trục lò xo luôn có phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm $t_{1} = 0,11 s$, điểm chính giữa của lò xo được giữ cố định, sau đó vật dao động điều hòa. Lấy g = 10 m/s2; π2 = 10. Biết độ cứng của lò xo tỉ lệ nghịch với chiều dài tự nhiên của nó. Thời điểm đầu tiên lực đàn hồi của lò xo bị triệt tiêu kể từ khi giữ cố định lò xo là

Đáp án án đúng là: A

Lời giải chi tiết:

+ Tốc độ của vật sau khoảng thời gian t = 0,11 s rơi tự do là $\Large{{v}_{0}}=gt=10.0,11=1,1$m/s.

+ Sau khi điểm chính giữa của lò xo được giữ cố định thì phần lò xo tham gia vào dao động có độ cứng $k = 2k_{0} = 25 N/m$.

→ Tần số góc của dao động $\Large \omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{25}{0,1}}=5\pi $ rad/s → T = 0,4 s.

+ Độ biến dạng của lò xo khi vật đi qua vị trí cân bằng $\Large \Delta {{l}_{0}}=\dfrac{mg}{k}=\dfrac{0,1.10}{25}=4$cm.

+ Biên độ dao động của con lắc $\Large A=\sqrt{\Delta l_{0}^{2}+{{\left( \dfrac{{{v}_{0}}}{{{\omega }^{2}}} \right)}^{2}}}=\sqrt{{{4}^{2}}+{{\left( \dfrac{110}{5\pi } \right)}^{2}}}=8$cm.

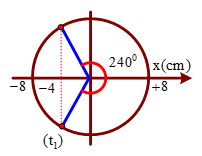
Hình đáp án 1. Một con lắc lò xo có m = 100 g và k = 12,5 N/m. Thời điểm ban đầu (t =

+ Tại $t_{1} = 0,11 s$ vật đang ở vị trí có li độ $\Large x=-\Delta {{l}_{0}}=-\dfrac{A}{2}=-4$ cm. Lực đàn hồi của lò xo bị triệt tiêu tại vị trí lò xo không biến dạng (tương ứng với $\Large x=-\Delta {{l}_{0}}$).

→ từ hình vẽ, t có $t={{t}_{1}}+\frac{2T}{3}=0,11+\frac{2}{3}.0,4=0,38$s.

 

Bài sau

Xem thêm các bài tiếp theo bên dưới