Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ thuộc thời gia

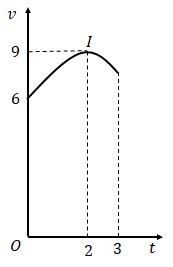
Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ thuộc thời gian (h) có đồ thị của vận tốc là một phần của đường parabol cố định I(2;9) và trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường mà vật di chuyển được trong 3 giờ đó

• A. s = 24, 25(km)
• B. s = 26,75(km)
• C. s= 24,75(km)
• D. s = 25,25 (km)

Ta đi tìm phương trình vận tốc của vật:
Theo giả thiết trong khoảng thời gian từ 0 đến 3 giờ vận tốc của vật là $\Large\mathrm{v(t) = at^2 + bt + c}$
Căn cứ vào đồ thị đã cho có
$\Large\left\{\begin{array}{l}v(0)=6 \\ t_{0}=-\dfrac{b}{2 a}=2 \\v(t_0) = 9\end{array}\right.\Leftrightarrow\left\{\begin{array}{l}c=6 \\ b=-4 a \\a(-\dfrac{b}{2a})^2 + b.(-\dfrac{b}{2a}) + c = 9\end{array} \quad \Leftrightarrow\left\{\begin{array}{l}a=-\dfrac{3}{4} \\ b=3 \\ c=6\end{array}\right.\right.$
Vậy $\Large v(t)=-\dfrac{3}{4} t^{2}+3 t+6,0 \leq t \leq 3$
Vậy $\Large s=\int_{0}^{3} v(t) d t=\int_{0}^{3}\left(-\dfrac{3}{4} t^{2}+3 t+6\right) d t=\dfrac{99}{4}=24,75$