Cho hàm số $\Large y=f(x)=m{{x}^{4}}+n{{x}^{3}}+p{{x}^{2}}+qx+r$ , tro

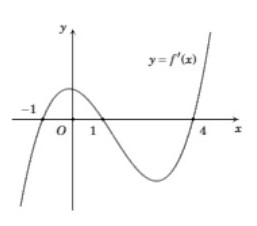
Cho hàm số $\Large y=f(x)=m{{x}^{4}}+n{{x}^{3}}+p{{x}^{2}}+qx+r$ , trong đó $\Large m,n,p,q,r\in R$ . Biết rằng hàm số $\Large y={f}'(x)$ có đồ thị như hình vẽ bên. Tập nghiệm của phương trình $\Large f(x)=16m+8n+4p+2q+r$ có tất cả bao nhiêu phần tử ?

• A.

  A. 4

• B.

  B. 3

• C.

  C. 5

• D.

  D. 6

Từ đồ thị ta thấy phương trình $\Large f'(x)=0$ có ba nghiệm phân biệt là $\Large x=-1, x=1$ và $\Large x=4$

Ta có bảng biến thiên

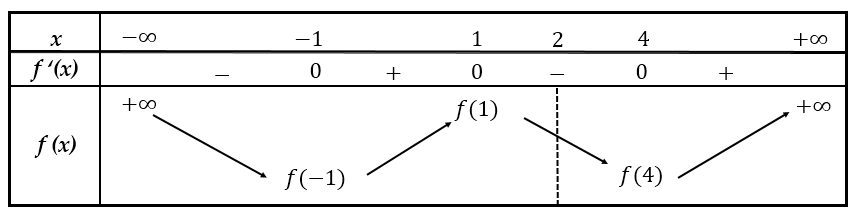
Phương trình $\Large f(x)= 16m+8n+4p+2q+r \Leftrightarrow f(x)=f(2). (1)$

Mặt khác, gọi $\Large S_1$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $\Large f'(x)$, trục hoành và hai đường thẳng $\Large x=-1, x=1$, ta có $\Large S_1=\int_{-1}^1f'(x)dx=f(1)-f(-1)$;

Gọi $\Large S_2$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số f'(x), trục hoành và hai đường thẳng x=1; x=4, ta có $\Large S_2=-\int_{1}^{4}f'(x)dx=f(1)-f(4)$.

Mà $\Large S_1f(4), (2)$

Từ (1), (2) và dựa vào bảng biến thiên ta thấy phương trình $\Large f(x)= 16m+8n+4p+2q+r$ có 4 nghiệm phân biệt 

Chọn đáp án A.