Một sóng cơ truyền trên sợi dây dài, nằm ngang, dọc theo chiều dương c

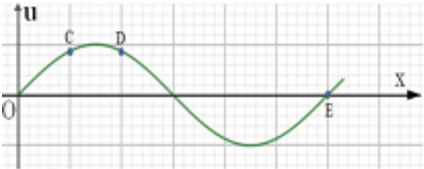
Một sóng cơ truyền trên sợi dây dài, nằm ngang, dọc theo chiều dương của trục Ox với tốc độ truyền sóng là v và biên độ không đổi. Tại thời điểm $\Large t_0=0$, phần tử tại O bắt đầu dao động từ vị trí cân bằng theo chiều âm của trục Ou. Tại thời điểm $\Large t_1 = 0,3 s$ hình ảnh của một đoạn dây như hình vẽ. Khi đó vận tốc dao động của phần tử tại D là $\Large v_D=\dfrac{\pi}{8}v$  và quãng đường phần tử E đã đi được là 24 cm. Biết khoảng cách cực đại giữa hai phần tử C, D là 5cm. Phương trình truyền sóng là 

• A. $\Large u=\cos\left(\dfrac{40\pi}{3}t-\dfrac{\pi x}{3}-\dfrac{\pi}{2}\right)cm$ (x tính bằng cm; t tính bằng s)
• B. $\Large u=\cos\left(20\pi t-\dfrac{\pi x}{3}+\dfrac{\pi}{2}\right)cm$ (x tính bằng cm; t tính bằng s)
• C. $\Large u=3\cos\left(20\pi t-\dfrac{\pi x}{12}+\dfrac{\pi}{2}\right)cm$ (x tính bằng cm; t tính bằng s)
• D. $\Large u=3\cos\left(\dfrac{40\pi}{3}t-\dfrac{\pi x}{3}+\dfrac{\pi}{2}\right)cm$ (x tính bằng cm; t tính bằng s)

Phương pháp: 
Thời điểm đầu tiên sóng bắt đầu từ 0 nên: $\Large u_O=A\cos\left(\omega t+\dfrac{\pi}{2}\right)cm$
Sau thời gian t = 0,3s, sóng có dạng như hình vẽ, điểm O lại đang ở VTCB và chuyển động về biên âm nên: $\Large t=0,3s=n.T$ 
Dễ thấy từ 0 đến E là một bước sóng ứng với 6 ô li, nên sóng truyền từ 0 đến E mất thời gian 1 chu kì T. Vì vậy quãng đường mà E đi được trong thời gian trên là: $\Large S=(n-1).4A$ 
Hai điểm C và D đều đang cách đỉnh sóng một khoảng nửa ô li nên biên độ của D là $\Large x_D=\dfrac{\sqrt{3}}{2}A$  và vận tốc của D lúc đó là $\Large v_D=\dfrac{1}{2}v_{max}=\dfrac{1}{2}\omega A$
Vận tốc sóng $\Large v=\lambda.f$
Khoảng cách giữa vtcb của C và D ứng với 1 ô li, khoảng cách giữa C và D là: $\Large CD=\sqrt{d^{2}+(u_C-u_D)^{2}}$
Lời giải: 
Thời điểm đầu tiên sóng bắt đầu từ O nên: $\Large u_O=A.\cos\left(\omega t+\dfrac{\pi}{2}\right)cm$

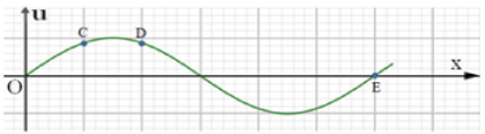
Sau thời gian t = 0,3s, sóng có dạng như hình vẽ, điểm O lại đang ở vtcb và chuyển động về biên âm nên: $\Large t=0,3s=n.T$ 
Dễ thấy từ O đến E là một bước sóng ứng với 6 ô li, nên sóng truyền từ O đến E mất thời gian 1 chu kì T. Vì vậy quãng đường mà E đi được trong thời gian trên là: $\Large S=(n-1).4A$
Hai điểm C và D đều đang cách đỉnh sóng một khoảng nửa ô li nên biên độ của D là $\Large x_D=\dfrac{\sqrt{3}}{2}A$ và vận tốc của D lúc đó là: 
$\Large v_D=\dfrac{1}{2}v_{max}=\dfrac{1}{2}\omega A\Rightarrow\dfrac{1}{2}\omega A=\dfrac{\pi}{8}v=\dfrac{\pi}{8}\lambda f=\dfrac{\pi}{8}\lambda.\dfrac{\omega}{2\pi}\Rightarrow \lambda=8A$
Ta có VTLG: 

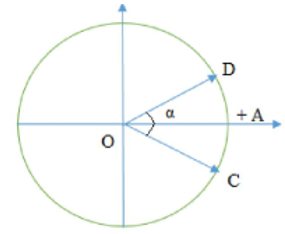
Khoảng cách giữa VTCB của C và D ứng với 1 ô li tức là $\Large CD=\dfrac{\pi}{6}$ và $\Large \alpha=\dfrac{\pi}{3}$ 
Khoảng cách giữa hai điểm C và D là: $\Large CD=\sqrt{d^{2}+(u_C-u_D)^{2}}$
Khoảng cách giữa hai điểm C và D cực đại là 5 cm khi $\Large (u_C-u_D)$ cực đại. 
 
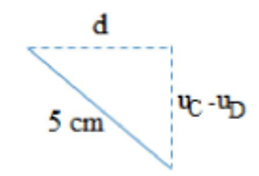
Ta có: $\Large u_C-u_D=A\cos\left(\omega t-\dfrac{\pi}{3}\right)\Rightarrow (u_C-u_D)_{max}=A$
$\Large CD=\sqrt{d^{2}+(u_C-u_D)^{2}}\Rightarrow 5=\sqrt{\left(\dfrac{\lambda}{6}\right)^{2}+(u_C-u_D)^{2}}=\sqrt{\left(\dfrac{8A}{6}\right)^{2}+A^{2}}\Rightarrow A=3cm\Rightarrow \lambda=8A=24cm$
Ta có: $\Large S=(n-1).4A=24 \Rightarrow n=3$
Lại có: $\Large t=0,3s=3T\Rightarrow T=0,1s\Rightarrow \omega=\dfrac{2\pi}{T}=20\pi(rad/s)$
Vậy ta có phương trình truyền sóng là: 
$\Large u=3\cos\left(20\pi t+\dfrac{\pi}{2}-\dfrac{2\pi x}{24}\right)=3\cos\left(20\pi t+\dfrac{\pi}{2}-\dfrac{\pi x}{12}\right)cm$
Chọn C.