Đặt điện áp xoay chiều $\Large u=U\sqrt{2}\cos(\omega t)(U,\omega$ là

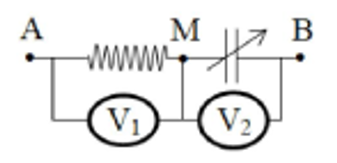
Đặt điện áp xoay chiều $\Large u=U\sqrt{2}\cos(\omega t)(U,\omega$ là các hằng số dương) vào hai đầu mạch điện như hình vẽ. Đoạn AM chứa cuộn dây không thuần cảm, đoạn MB chứa tụ điện có điện dung C thay đổi được, các vôn kế lí tưởng. Khi C có giá trị để vôn kế $\Large V_2$ chỉ giá trị lớn nhất thì tổng số chỉ hai vôn kế là 36V. Khi C có giá trị để tổng số chỉ hai vôn kế lớn nhất thì tổng này là $\Large 24\sqrt{3}V$. Giá trị của U bằng

 

• A. $\Large 24 V$
• B. $\Large 12\sqrt{6}V$
• C. $\Large 12\sqrt{3}V$
• D. $\Large 12 V$

Phương pháp: 
Khi C có giá trị để vôn kế V2 chỉ giá trị lớn nhất tức là $\Large U_{Cmax}$ thì tổng số chỉ hai vôn kế là: 
 $\Large U_{LR}+U_{Cmax}=36V$
Khi C có giá trị để tổng số chỉ hai vôn kế lớn nhất thì tổng này là  $\Large (U_{RL}+U_C)_{max}=24\sqrt{3}V$
Sử dụng phương pháp giản đồ vecto: 
    + Khi $\Large U_{Cmax}$ thì $\Large U_{LR}$ vuông pha với U 
    + Khi $\Large (U_{RL}+U_C)_{max}$ thì ta có giản đồ $\Large U_{RL}=U_C$ 
Vì R và L không đổi nên góc giữa $\Large U_{RL}$ và $\Large U_C$ không đổi. 
Lời giải: 
Khi C có giá trị để vôn kế V2 chỉ giá trị lớn nhất tức là $\Large U_{Cmax}$ thì tổng số chỉ hai vôn kế là: $\Large U_{LR}+U_{Cmax}=36V$  
Khi $\Large U_{Cmax}$ thì $\Large U_{LR}$ vuông pha với U 
 
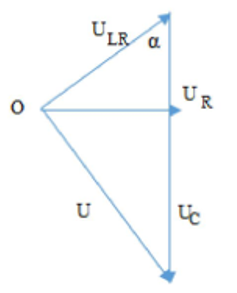
Từ hình vẽ ta có: $\Large \left\{\begin{align}&U^{2}=U_C^{2}-U_{RL}^{2}=U_C^{2}-(36-U_C)^{2}\\&\cos\alpha=\dfrac{U_{RL}}{U_C}=\dfrac{36-U_C}{U_C}\\\end{align}\right.$

Khi C có giá trị để tổng số chỉ hai vôn kế lớn nhất thì tổng này là: $\Large (U_{RL}+U_C)_{max}=24\sqrt{3}V$
Khi $\Large (U_{RL}+U_C)_{max}$ thì ta có giản đồ $\Large U_{RL}=U_C=12\sqrt{3}V$ 
 
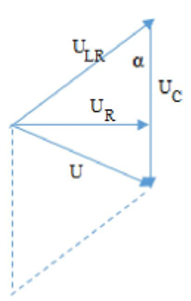
Ta có $\Large U^{2}=U_C^{2}+U_{RL}^{2}-2U_C.U_{RL}.\cos(\alpha)$
Vì R và L không đổi nên góc giữa $\Large U_{RL}$ và $\Large U_C(\alpha)$ không đổi. 
Ta có: $\Large U^{2}=U_C^{2}+U_{RL}^{2}-2U_C.U_{RL}.\cos(\alpha)\Rightarrow U^{2}_C-(36-U_C)^{2}=2(12\sqrt{3})^{2}-2(12\sqrt{3})^{2}.\dfrac{36-U_C}{U_C}$
$\Large \left[\begin{align}&U_C=18V\\&U_C=24V\\\end{align}\right.$ $\Large \Rightarrow \left[\begin{align}&U^{2}=U_C^{2}-(36-U_C)^{2}=0\\&U^{2}=U_C^{2}-(36-U_C)^{2}=(12\sqrt{3})^{2}\\\end{align}\right.$ $\Large \Rightarrow U=12\sqrt{3}V$
Chọn C.