Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng

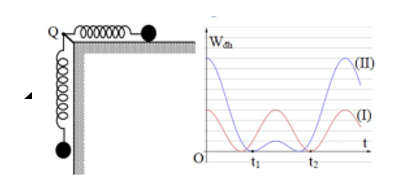
Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định gắn chung tại điểm Q. Con lắc (I) nằm ngang trên mặt bàn nhẵn. Con lắc (II) treo thẳng đứng cạnh mép bàn như hình vẽ. Kích thích cho hai con lắc dao động điều hòa tự do. Chọn mốc thế năng đàn hồi của mỗi con lắc tại các vị trí tương ứng của vật lúc lò xo có chiều dài tự nhiên. Thế năng đàn hồi các con lắc phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ. Biết tại thời điểm t = 0, cả hai lò xo đều dãn và $\Large t_2-t_1=\dfrac{\pi}{12}s$. Lấy $\Large g=10m/s^{2}$. Tại thời điểm $\Large t=\dfrac{\pi}{10}s$, khoảng cách hai vật dao động gần nhất với giá trị nào sau đây? 

• A. 85 cm.
• B. 125 cm.
• C. 149 cm.
• D. 92 cm.

Phương pháp: 
Công thức tính thế năng: $\Large W_t=\dfrac{1}{2}kx^{2}$
Tần số góc: $\Large \omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{g}{\Delta l_0}}$
Sử dụng VTLG. 
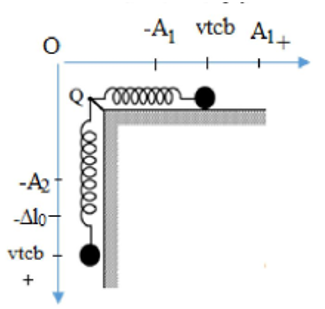
Lời giải: Ta có hình vẽ, chọn hệ quy chiếu như hình vẽ: 

Đồ thị thế năng đàn hồi của hai con lắc: 
 
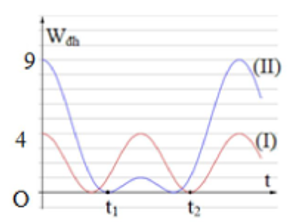
Từ đồ thị ta thấy đường màu đỏ cho biết thế năng đàn hồi của con lắc lò xo nằm ngang. Thế năng cực đại ứng với 4 đơn vị $\Large W_1=\dfrac{1}{2}.kA_1^{2}$
Đường màu xanh là thế năng đàn hồi của con lắc lò xo treo thẳng đứng. Vì tại vị trí cân bằng lò xo đã dãn một đoạn $\Large \Delta l_0$  nên tại vị trí lò xo dãn nhiều nhất, thế năng đàn hồi cực đại lớn nhất ứng với 9 đơn vị: 
$\Large W_{2+}=\dfrac{1}{2}.k(A+\Delta l_0)^{2}$
Tại vị trí biến trên (biên âm) thì thế năng đàn hồi ứng với 1 đơn vị: $\Large W_{2-}=\dfrac{1}{2}k(A-\Delta l_0)^{2}$
Ta có tỉ số: 
$\Large \left\{\begin{align}&\dfrac{W_{2+}}{W_{2-}}=\dfrac{9}{1}=\dfrac{(A_2+\Delta l_0)^{2}}{A_2-\Delta l_0)^{2}}\Leftrightarrow \dfrac{(A_2+\Delta l_0)}{(A_2-\Delta l_0)}=3\Rightarrow A_2=2\Delta l_0\\&\dfrac{W_{2+}}{W_1}=\dfrac{9}{4}=\dfrac{(A_2+\Delta l_0)^{2}}{A_1^{2}}\Leftrightarrow \dfrac{A_2+\Delta l_0}{A_1}=\dfrac{3}{2}\Leftrightarrow \dfrac{3\Delta l_0}{A_1}=\dfrac{3}{2}\Rightarrow A_1=2\Delta l_0=A_2\\\end{align}\right.$
Tại thời điểm ban đầu t = 0, ta thấy cả hai vật đều đang ở biên cương. Thời điểm t là thời điểm vật của lò xo treo thẳng đứng đi qua vị trí lò xo không dãn. 
Ta có VTLG 
 
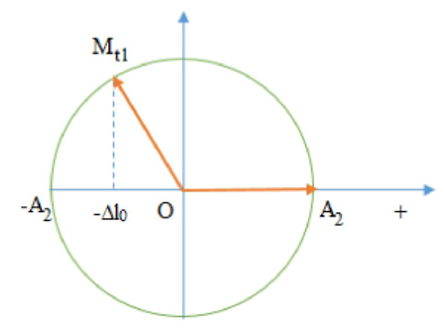
Thời gian từ t = 0 đến $\Large t_1$ là $\Large t_1=\dfrac{T}{2\pi}\left(\dfrac{\pi}{2}+arcsin\dfrac{\Delta l_0}{A_2}\right)=\dfrac{T}{3}$ 
Thời điểm $\Large t_2$ là thời điểm vật của lò xo nằm ngang đi qua vị trí cân bằng lần thứ 2. Ta có VTLG: 
 
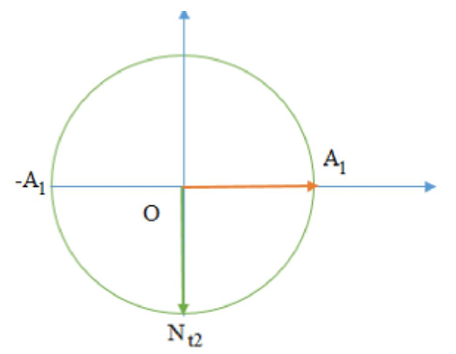
Thời gian từ t = 0 đến $\Large t_2$ là $\Large t_2=\dfrac{3}{4}T$ 
Khoảng thời gian $\Large t_2-t_1=\dfrac{\pi}{12}\Rightarrow \dfrac{3}{4}T-\dfrac{T}{3}=\dfrac{5}{12}T=\dfrac{\pi}{12}\Rightarrow T=\dfrac{\pi}{5}(s)$
Tần số góc của hai con lắc là như nhau vì chúng đều dao động tự do và có cùng độ cứng, vật nặng cùng khối 
lượng: $\Large \omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{g}{\Delta l_0}}$
Vậy ta có: $\Large \omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{\pi}{5}}=10=\sqrt{\dfrac{g}{\Delta l_0}}\Rightarrow \Delta l_0=0,1m=10cm$
$\Large \Rightarrow A_1=A_2=20cm$
Sau thời gian $\Large t=t=\dfrac{\pi}{10}s=\dfrac{T}{2}$ thì hai vật đều đang ở biên âm. 
Khoảng cách giữa hai vật lúc này là: 
 $\Large d=\sqrt{(l-A_1)^{2}+(l+\Delta l_0-A_2)^{2}}=\sqrt{(80-20)^{2}+(80+10-20)^{2}}=92,2cm$
Chọn D.