Một lò xo nhẹ dài 60 cm, có độ cứng k = 100 N/m được treo vào một điểm

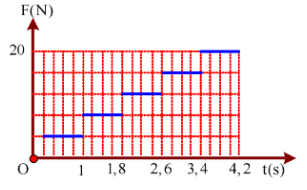
Một lò xo nhẹ dài 60 cm, có độ cứng k = 100 N/m được treo vào một điểm cố định ở độ cao h = 1 m so với mặt đất, đầu dưới treo vật nhỏ khối lượng m = 400 g. Giữ vật ở vị trí lò xo không biến dạng rồi buông nhẹ để vật dao động điều hòa tự do dọc theo trục lò xo. Chọn trục tọa độ thẳng đứng chiều dương hướng xuống, gốc thời gian là lúc buông vật. Tại thời điểm t = 0,2 s, một lực $ \overrightarrow{F}$ thẳng đứng, có cường độ biến thiên theo thời gian biểu diễn như đồ thị trên hình bên, tác dụng vào vật. Biết điểm treo chỉ chịu được lực kéo tối đa có độ lớn 20 N. Bỏ qua khối lượng của lò xo và sức cản không khí. Vận tốc của vật khi chạm đất là:

• A.

  $ 20 \pi \sqrt{3} cm/s$.

• B.

  $ 2,28 cm/s$.

• C.

  $ 20 \pi cm/s$.

• D.

  $ 40 \pi cm/s$.

Hướng dẫn:

+ Tần số góc của hệ dao động $ \omega = \sqrt{\dfrac{k}{m}} = \sqrt{\dfrac{100}{0,4}} = 5\pi rad/s \rightarrow T = 0,4s$

+ Độ biến dạng của lò xo tại vị trí cân bằng $ \Delta l_{0} = \dfrac{mg}{k} = \dfrac{0,4.10}{100} = 4cm$

Lực kéo tác dụng vào điểm treo $ F_{max} = k(\Delta l_{0} + x) \leq 20N \rightarrow A_{max = 16cm}$

Để đơn giản, ta có thể mô tả chuyển động của vật theo từng khoảng thời gian như sau:

  - Từ thời điểm ban đầu đến t = 0,2 s: vật dao động điều hòa quanh vị trí cân bằng O với biên độ $ A_{0} = 4 cm$. Tại thời điểm t = 0,2 s vật đến biên dương $ \rightarrow x_{02} = 4cm; v_{0,2} = 0$

  - Từ 0,2 s đến 1 s: dưới tác dụng của ngoại lực F = 4 N con lắc dao động quanh vị trí cân bằng mới $ O_{1}$, dưới O một đoạn $ \Delta x_{0} = \dfrac{F}{k} = \dfrac{4}{100} = 4cm$, trùng với $ x_{02} \rightarrow$ trong khoảng thời gian này con lắc nằm yên tại $ O_{1}$

  - Từ 1 s đến 1,8 s: dưới tác dụng của ngoại lực F = 8 N con lắc dao động quanh vị trí cân bằng mới $ O_{2}$, dưới $ O_{1}$ một đoạn $ \Delta x_{0} = \dfrac{F}{k} = \dfrac{4}{100} = 4 cm$ với biên độ $ A_{2} = \Delta x_{0}$. Ta lưu ý rằng $ \Delta t = 1,8 - 1 = 0,8s = 2T \rightarrow $ tại thời điểm t = 1,8s con lắc quay về vị trí $ O_{1}$, tại vị tí này tốc độ của vật $ v_{1,8} = 0$.

  - Từ 1,8 s đến 2,6 s: dưới tác dụng của lực điện F = 12 N, con lắc dao động quanh vị trí cân bằng mới $ O_{3}$, dưới $ O_{2}$ một đoạn $ \Delta x_{0}$ với biên độ $ A_{3} = 2\Delta x_{0} = 8cm$

Ta chú ý rằng, khi con lắc đi qua vị trí $ x_{3} = 0,5 A_{3} \rightarrow v_{3} = \dfrac{\sqrt{3}}{2}v_{3}max = \dfrac{\sqrt{3}}{2}\omega A_{3} \approx 1,09 m/s$  lò xo giãn một đoạn 20 cm $ \rightarrow$ con lắc rời khỏi giá đỡ chuyển động thẳng đứng xuống dưới.

$ \rightarrow$ Áp dụng bảo toàn cơ năng. Vận tốc của vật khi chạm đất là $ v = \sqrt{1,09^{2}+2.10(1-0,6-0,2)} = 2,28 m/s$