Tại mặt chất lỏng, hai nguồn $ S_{1}, S_{2}$ cách nhau 13 cm dao động

Tại mặt chất lỏng, hai nguồn $ S_{1}, S_{2}$ cách nhau 13 cm dao động theo phương thẳng đứng với phương trình $ u_{1} = u_{2} = Acos40\pi t$ cm (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 80 cm/s. Ở mặt chất lỏng, gọi $ \Delta$ là đường trung trực của $ S_{1}S_{2}$. M là một điểm không nằm trên $ S_{1}S_{2}$ và không thuộc $ \Delta$, sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và ngược pha với hai nguồn. Khoảng cách ngắn nhất từ M đến $ \Delta$ là

• A. 2,00 cm.
• B. 2,64 cm.
• C. 2,46 cm.
• D. 4,92 cm.

Hướng dẫn:

Bước sóng của sóng $ \lambda = \dfrac{2 \pi v}{\omega} = \dfrac{2 \pi.80}{40 \pi} = 4cm$

+ M cực đại và ngược pha với nguồn thì $ \left\{\begin{array}{l} d_{2}-d_{1} = k \lambda \\ d_{1} + d_{2} = n \lambda \end{array}\right.$ với n, k không cùng chẵn hoặc không cùng lẻ.

Để M gần $ \Delta$ nhất $ \rightarrow k = 1$, n khi đó có thể nhận các giá trị 2, 4, 6…..thõa mãn bất đẳng thức tam giác

$ d_{1}+d_{2} > 13 \rightarrow n > \dfrac{13}{\lambda} = 3,25 \rightarrow n_{min} = 4$

$ \left\{\begin{array}{l} d_{2} - d_{1} = 4 \\ d_{1} + d_{2} = 16 \end{array}\right. 
 cm \rightarrow \left\{\begin{array}{l} d_{2} = 10 \\ d_{1} = 6  \end{array}\right. cm$

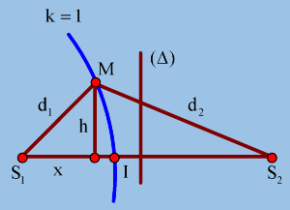
Từ hình vẽ: $ \left\{\begin{array}{l}  6^{2} = x^{2} + h^{2}\\ 10^{2} = (13-x)^{2} + h^{2} \end{array}\right. \rightarrow x = 4,04 cm$

Vậy khoảng cách giữa M và $ \Delta$ khi đó là $ \dfrac{13}{2} - 4,04 = 2,46$