Đặt điện áp xoay chiều ổn định $ u = U_{0}cos100 \pi t$ V vào hai đầu

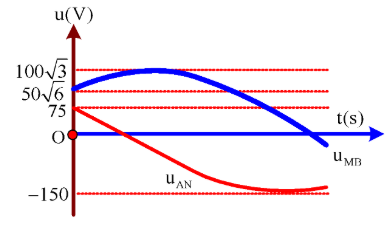
Đặt điện áp xoay chiều ổn định $ u = U_{0}cos100 \pi t$ V vào hai đầu đoạn mạch AB gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần R và tụ điện có điện dung $ C = \dfrac{5.10^{-4}}{\pi}$ F mắc nối tiếp theo đúng thứ tự trên. Gọi M là điểm nối giữa cuộn cảm và điện trở, N là điểm nối giữa điện trở và tụ điện. Đồ thị biểu diễn sự phụ thuộc vào thời gian của điện áp giữa hai đầu đoạn mạch AN và điện áp giữa hai đầu đoạn mạch MB như hình vẽ. Công suất tiêu thụ của đoạn mạch gần với giá trị nào nhất sau đây?

• A. 700 W.
• B. 350 W.
• C. 375 W.
• D. 188 W.

Hướng dẫn:

Dung kháng của tụ điện $ Z_{C} = 20 \Omega$

+ Từ hình vẽ ta có: $ \left\{\begin{array}{l} u_{AN} = 150cos(\omega t + \dfrac{\pi}{3}) \\ 
u_{MB} = 100 \sqrt{3} cos (\omega t - \dfrac{\pi}{4}) V \rightarrow \varphi_{AN} - \varphi_{MB} = 105^{o} \end{array}\right.$

+ Công suất tiêu thụ trên AN cũng chính là công suất tiêu thụ trên MB và trên toàn  mạch $ U_{AN}Icos \varphi_{AN} = U_{MB}I cos \varphi_{MB} \rightarrow \dfrac{cos \varphi_{MB}}{cos \varphi_{AN}} = \dfrac{U_{AN}}{U_{MB}} = \dfrac{\sqrt{3}}{2} \Leftrightarrow \dfrac{cos \varphi_{MB}}{cos(\varphi_{AB}+105^{o})} = \dfrac{\sqrt{3}}{2} \rightarrow \varphi_{MB} \approx 124,35^{o}$

+ Ta có : $ tan \varphi_{MB} = -\dfrac{Z_{C}}{R} \rightarrow R = -\dfrac{Z_{C}}{tan \varphi_{MN}} \approx 13,67 \Omega$

Suy ra công suất tiêu thụ của mạch $ P = \dfrac{U^{2}_{MB}}{R}cos^{2}\varphi_{MB} = \dfrac{(50 \sqrt{6})^{2}}{13,67} cos^{2}(124,35^{o}) \approx 349,4 W$