Một hình nón có đường kính đáy là $\large 2a\sqrt{3}$, góc ở đỉnh là $

Một hình nón có đường kính đáy là $\large 2a\sqrt{3}$, góc ở đỉnh là $\large 120^{\circ}$. Tính thể tích của khối nón đó theo a.

• A.

  A. $\large 3\pi a^{3}$

• B.

  B. $\large \pi a^{3}$

• C.

  C. $\large 2\sqrt{3}\pi a^{3}$

• D.

  D. $\large \pi a^{3}\sqrt{3}$

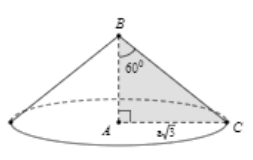
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy. Theo giả thiết dễ suy ra đường tròn đáy có bán kính $\large R = OA = a\sqrt{3}$ (cm) và góc $\large \widehat{ASO} = \dfrac{120^{\circ}}{2} = 60^{\circ}$ 

Xét tam giác SOA vuông tại O, ta có $\large SO = \dfrac{OA}{tan60^{\circ}} = \dfrac{a\sqrt{3}}{\sqrt{3}} = a$. Do đó chiều cao hình nón là h = a.

Vậy thể tích khối nón là $\large V = \dfrac{1}{3}\pi R^{2}h = \dfrac{1}{3}\pi .3a^{2}.a = \pi a^{3}$ .