Một con lắc lò xo treo thẳng đứng. Từ vị trí cân bằng, kéo vật nhỏ của

Một con lắc lò xo treo thẳng đứng. Từ vị trí cân bằng, kéo vật nhỏ của con lắc theo phương thẳng đứng xuống đến vị trí lò xo dãn 8 cm rồi buông ra, đồng thời truyền cho vật vận tốc 15π cm/s hướng về vị trí cân bằng. Con lắc dao động điều hòa với chu kì 0,4 s. Lấy g = 10 m/s²; π² = 10. Trong một chu kì dao động, khoảng thời gian mà độ lớn lực đàn hồi của lò xo không nhỏ hơn 0,6 lần độ lớn lực kéo về là ∆t. Giá trị của ∆t gần giá trị nào nhất sau đây?  

• A.

  A. 0,125 s.

• B.

  B. 0,315 s.

• C.

  C. 0,285 s.

• D.

  D. 0,265 s.

$\Large T=0,4s\Rightarrow \omega =5\pi \left( \dfrac{rad}{s} \right),\Delta {{\ell }_{0}}=\dfrac{mg}{k}=\dfrac{g}{{{\omega }^{2}}}=4cm$

$\Large \Rightarrow A=\sqrt{{{x}^{2}}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}$, Dãn $8cm\Rightarrow \left| x \right|=4cm$

$\Large \Rightarrow A=5cm$

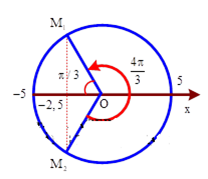
$\Large{{F}_{dh}}\ge 0,6{{F}_{kv}}$ Chon  $Ox\downarrow \Rightarrow {{\left( x+4 \right)}^{2}}\ge 0,36{{x}^{2}}\Rightarrow -2,5\le x\le 5$

+ Trong một chu kì: $\Large \Delta t=\dfrac{2}{3}T=\dfrac{4}{15}s\approx 0,267s$