Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng $\Large k=25N/m,

Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng $\Large k=25N/m,$ một đầu gắn với hòn bi nhỏ khối lượng $\Large m =100g.$ Khi vật đang ở vị trí cân bằng, tại thời điểm $\Large t = 0$ người ta thả cho con lắc rơi tự do sao cho trục lò xo luôn nằm theo phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm $\Large t_1=0,11s$ thì đầu trên của lò xo được giữ cố định. Lấy $\Large g=10m/s^2.$ Bỏ qua ma sát, lực cản. Tốc độ của hòn bị tại thời điểm $\Large t_2=t_1+0,1s$ gần nhất với giá trị nào sau đây?

• A. A. 120 cm/s.
• B. B. 90 cm/s.
• C. C. 100 cm/s.
• D. D. 60 cm/s.

Phương pháp:
+ Sử dụng biểu thức tính tần số góc: $\Large \omega=\sqrt{\dfrac{k}{m}}$
+ Sử dụng biểu thức xác định vận tốc vật rơi tự do: $\Large v=gt$
+ Sử dụng hệ thức độc lập: $\Large A^2=x^2+\dfrac{v^2}{\omega^2}$
+ Sử dụng vòng tròn lượng giác
Cách giải:
+ Tần số góc của dao động: $\Large \omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{25}{100.10^{-3}}}=5\pi rad/s \Rightarrow T=\dfrac{2\pi}{\omega}=0,4s$
+ Tốc độ của con lắc sau khoảng thời gian rơi tự do: $\Large v=gt=10.0,11=1,1m/s$
+ Sau khi đột ngột giữ lại đầu trên của con lắc thì con lắc sẽ dao động quanh vị trí cân bằng của lò xo. 
Tại vị trí giữa này lò xo giãn một đoạn $\Large \Delta l=\dfrac{mg}{k}=\dfrac{0,1.10}{25}=0,04m=4cm$
Biên độ dao động mới của con lắc là: $\Large A=\sqrt{\Delta l^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,04^2+\dfrac{1,1^2}{(5\pi)^2}}=0,0806m=8,06cm$ 
Khoảng thời gian $\Large \Delta t=t_2-t_1=0,1s=\dfrac{T}{4}$
Góc quét: $\Large \Delta \varphi=\dfrac{\pi}{2},$ vẽ trên vòng tròn lượng giác ta được:

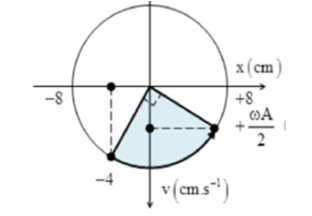
$\Large \Rightarrow$ Vận tốc của vật khi đó: $\Large v=\dfrac{v_{max}}{2}=\dfrac{A\omega}{2}=\dfrac{8,06.(5\pi)}{2}=63,303 cm/s$
Chọn D.