Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp một điện áp xoay chiều $\La

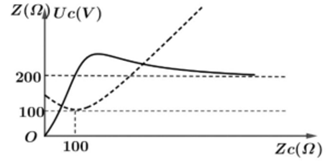
Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp một điện áp xoay chiều $\Large u=U_0cos\omega t (V),$ thay đổi C thì thấy điện áp hiệu dụng hai đầu đoạn mạch chứa tụ điện C (nét liền) và tổng trở của mạch (nét đứt) có dạng như hình vẽ. Giá trị của $\Large U_{Cmax}$ gần nhất giá trị nào sau đây?

• A. A. 100V.
• B. B. 281V.
• C. C. 282V.
• D. D. 283V.

Phương pháp:
 Sử dụng bài toán C biến thiên để 
+ $\Large Z_{min}$ khi đó $\Large Z_L=Z_C$ 
+ $\Large Z_C \rightarrow \infty$ khi đó $\Large U_C=U$
+ $\Large U_{C_{max}}$ khi đó: $\Large U_{C_{max}}=\dfrac{U\sqrt{R^2+Z_L^2}}{Z_L}$ 
Cách giải:
Từ đồ thị, ta có: $\Large Z_{min}=100\Omega$ khi $\Large Z=100\Omega$  
Mà ta có, C biến thiên $\Large Z_{min}$ khi đó $\Large Z_C=Z_L=100\Omega$ và $\Large Z_{min}=R=100\Omega$ 
Lại có: $\Large U_C=\dfrac{U}{\sqrt{\dfrac{R^2+Z_L^2}{Z_C^2}-\dfrac{2Z_L}{Z_C}+1}}$
Khi $\Large Z_C \rightarrow \infty$ thì $\Large U_C=U$ 
Từ đồ thị, ta suy ra $\Large U=200V$
+ C biến thiên để $\Large U_{C_{max}}=\dfrac{U\sqrt{R^2+Z_L^2}}{Z_L}=\dfrac{200\sqrt{100^2+100^2}}{100}=200\sqrt{2}V$
Chọn D.