Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng

Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm A cách 0 một đoạn $\Large x (m).$ Trên tia vuông góc với OA tại A lấy điểm B cách A một khoảng $\Large 6m.$ Điểm M thuộc đoạn AB sao cho $\Large AM=4,5m.$ Thay đổi x để góc MOB có giá trị lớn nhất, khi đó mức cường độ âm tại A là $\Large L_A=40 dB.$ Để mức cường độ âm tại M là $\Large 50 dB$ thì cần đặt thêm tại O bao nhiêu nguồn âm nữa? Coi các nguồn âm là hoàn toàn giống nhau.
 

• A. A. 35.
• B. B. 25.
• C. C. 15.
• D. D. 33.

Phương pháp:
+ Sử dụng công thức $\Large tan(\alpha_1-\alpha_2)=\dfrac{tan\alpha_1-tan\alpha_2}{1+tan\alpha_1.tan\alpha_2}$ và BĐT côsi
+ Sử dụng công thức: Hiệu mức cường độ âm: $\Large L_A-L_M=10\mathrm{log}\dfrac{I_A}{I_M}$
+ Sử dụng công thức tính cường độ âm: $\Large I=\dfrac{2P}{4\pi R^2}$
Cách giải:
$\Large OA=x (m); AB=6 (m); AM=4,5 (m)$ 

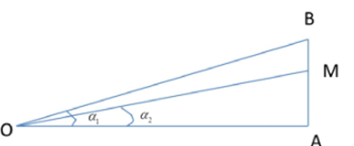
$\Large tanMOB=tan(\alpha_1-\alpha_2)=\dfrac{tan\alpha_1-tan\alpha_2}{1+tan\alpha_1 tan\alpha_2}=\dfrac{\dfrac{6}{x}-\dfrac{4,5}{x}}{1+\dfrac{6}{x}.\dfrac{4,5}{x}}=\dfrac{1,5}{d+\dfrac{27}{x}}$
Theo BĐY Cosi, ta có: $\Large x+\dfrac{27}{x} \geq 2\sqrt{27}=2.3\sqrt{3} \Rightarrow x=3\sqrt{3}m$
Do đó: $\Large OM=\sqrt{(3\sqrt{3})^2+4,5^2}=\dfrac{3\sqrt{21}}{2}m$
Ta có: $\Large L_A-L_M=10\mathrm{log}\dfrac{I_A}{I_N} \leftrightarrow 40-50=-10=10\mathrm{log}\dfrac{I_A}{I_M} \rightarrow \dfrac{I_A}{I_M}=0,1$
Mặt khác: $\Large \left\{\begin{align} & I_A=\dfrac{2P}{4\pi R_A^2} \\ & I_M=\dfrac{(n+2)P}{4\pi R^2_M} \end{align}\right.$ $\Large \Rightarrow \dfrac{I_A}{I_M}=\dfrac{2}{n+2}\dfrac{\bigg(\dfrac{3\sqrt{21}}{2}\bigg)^2}{(3\sqrt{3})^2}=0,1 \Rightarrow n=33$

Chọn D.