Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào ha

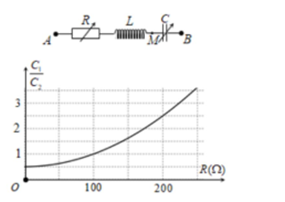
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch AB, trong đó R là biến trở, cuộn cảm thuần có hệ số tự cảm L, tụ điện có điện dung C thay đổi được. Khi $\Large C=C_1$ thì điện áp hai đầu đoạn mạch AM không phụ thuộc vào giá trị của R. Khi $\Large C=C_2$ thì điện áp hiệu dụng giữa hai đầu đoạn mạch MB đạt giá trị cực đại. Hình bên là đồ thị biểu diễn sự phụ thuộc của tỉ số $\Large \dfrac{C_1}{C_2}$ theo R. Giá trị của cảm kháng $\Large Z_L$ là:

• A.

  A. $\Large 150\Omega.$

• B.

  B. $\Large 200\Omega.$

• C.

  C. $\Large 100\Omega.$

• D.

  D. $\Large 50\Omega.$

Phương pháp:
Vận dụng các bài toán C biến thiên
Cách giải:
+ Khi $\Large C=C_1: U_{RL}$ không phụ thuộc vào R khi đó: $\Large Z_{C_{1}}=2Z_L$
+ Khi $\Large C=C_2: U_{C_{max}}$ khi đó $\Large Z_{C_{2}}=\dfrac{R^2+Z_L^2}{Z_L}$  
Xét tỉ số: $\Large \dfrac{C_1}{C_2}=\dfrac{Z_{C_{2}}}{Z_{C_{1}}}=\dfrac{R^2+Z_L^2}{2Z_L^2} \ (*)$
Từ đồ thị, tại điểm $\Large \dfrac{C_1}{C_2}=1$ ta có $\Large R=100\Omega$ 
Thay vào (*) suy ra $\Large Z_L=100 \Omega$  
Chọn C.