Một sợi dây dài 40cm đang có sóng dừng, ngoài hai đầu dây cố định trên

Một sợi dây dài 40cm đang có sóng dừng, ngoài hai đầu dây cố định trên dây còn có 3 điểm khác đứng yên, tần số dao động của sóng trên dây là 25Hz . Biết trong quá trình dao động tại thời điểm sợi dây duỗi thẳng thì tốc độ của điểm bụng khi đó là $\Large 1,5\pi m/s.$ Gọi x, y lần lượt là khoảng cách lớn nhất và nhỏ nhất giữa hai phần tử dây tại hai điểm bụng gần nhau nhất trong quá trình dao động. Tỉ số x/y bằng

• A. A. 1,17.
• B. B. 1,56.
• C. C. 1,42.
• D. D. 1,04.

Phương pháp:
+ Sử dụng biểu thức sóng dừng trên dây 2 đầu cố định: $\Large l=k\dfrac{\lambda}{2}$
+ Sử dụng biểu thức khoảng cách giữa hai điểm trong sóng dừng
Cách giải:
Số nút sóng 3 + 2 = 5 $\Large \Rightarrow$ Số bụng sóng k = 4

$\Large l=40cm=0,4m=4\dfrac{\lambda}{2} \Rightarrow \lambda=0,2m=20cm$

Ta có: $\Large v_{max}=1,5\pi =\omega A_b \Rightarrow A_b=0,03m=3cm$
Xét hai tử dây tại 2 điểm bụng gần nhau nhất trong quá trình dao động

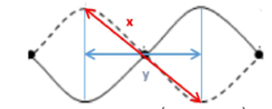
+ Khoảng cách nhỏ nhất của hai phần tử dây tại 2 điểm bụng gần nhau nhất trong quá trình dao động: y = 10cm (khi 2 điểm ở vị trí cân bằng) 
+ Khoảng cách lớn nhất của hai phần tử dây tại 2 điểm bụng gần nhau nhất trong quá trình dao động: $\Large x=\sqrt{10^2+6^2}=2\sqrt{34}cm$ (khi 2 điểm ở vị trí biên)

$\Large \Rightarrow$ Tỉ số $\Large \dfrac{x}{y}=\dfrac{2\sqrt{34}}{10}=1,17$ 
Chọn A.