Một con lắc đơn dao động điều hòa tại nơi có gia tốc trọng trường $\la

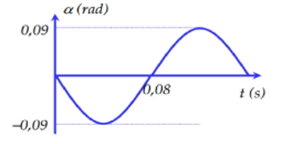
Một con lắc đơn dao động điều hòa tại nơi có gia tốc trọng trường $\large g = 10 m/s^2$, đồ thị biểu diễn sự phụ thuộc giữa li độ góc $\large \alpha $ và thời gian như hình vẽ. Lấy $\large {{\pi }^{2}}$ = 10, tốc độ lớn nhất của con lắc gần đúng bằng 

• A. A. 2,53 m/s.
• B. B. 0,023 m/s.
• C. C. 0,46 m/s.
• D. D. 1,27 m/s.

Phương pháp: 
Phương trình li độ góc, li độ cong và vận tốc của con lắc đơn là $\large \left\{ \begin{align}& \alpha ={{\alpha }_{0}}.\cos \left( \omega t+\varphi  \right) \\ & s=l{{\alpha }_{0}}.\cos \left( \omega t+\varphi  \right) \\ & v=s'=l{{\alpha }_{0}}.\omega .\cos \left(\omega t+\varphi +\dfrac{\pi }{2} \right) \\ \end{align} \right.$
Từ đồ thị ta tìm được chu kì T và biên độ góc 
Chu kì của dao động: $\large T=2\pi \sqrt{\dfrac{l}{g}}\Rightarrow l=\dfrac{{{T}^{2}}.g}{4{{\pi }^{2}}}$
Vận tốc lớn nhất của dao động là: $\large {{v}_{max}}=l{{\alpha }_{0}}.\omega =l{{\alpha }_{0}}.\dfrac{2\pi }{T}=\dfrac{{{T}^{2}}.g}{4{{\pi }^{2}}}.{{\alpha }_{0}}.\dfrac{2\pi }{T}=\dfrac{T.g.{{\alpha }_{0}}}{2\pi }$
Lời giải: 

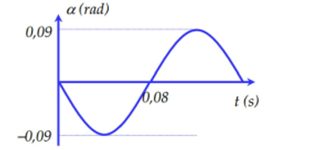
Từ đồ thị ta thấy nửa chu kì là 0,08s, vậy chu kì T = 0,16s. 
Biên độ của góc là: $\large {{\alpha }_{0}}=0,09rad$
Ta có các phương trình: $\large \left\{ \begin{align}& \alpha ={{\alpha }_{0}}.\cos \left( \omega t+\varphi  \right) \\ & s=l{{\alpha }_{0}}.\cos \left( \omega t+\varphi  \right) \\ & v=s'=l{{\alpha }_{0}}.\omega .\cos \left( \omega t+\varphi +\dfrac{\pi }{2} \right) \\ 
\end{align} \right.$

Chu kì của dao động: $\large T=2\pi \sqrt{\dfrac{l}{g}}\Rightarrow l=\dfrac{{{T}^{2}}.g}{4{{\pi }^{2}}}$
Vận tốc lớn nhất của dao động là: $\large {{v}_{max}}=l{{\alpha }_{0}}.\omega =l{{\alpha }_{0}}.\dfrac{2\pi }{T}=\dfrac{{{T}^{2}}.g}{4{{\pi }^{2}}}.{{\alpha }_{0}}.\dfrac{2\pi }{T}=\dfrac{T.g.{{\alpha }_{0}}}{2\pi }=\dfrac{0,16.10.0,09}{2\pi }=0,023m/s$

Chọn B.