Một con lắc đơn có chiều dài 50 cm dao động điều hòa tại nơi có $\Larg

Một con lắc đơn có chiều dài 50 cm dao động điều hòa tại nơi có $\Large g=9,8 \dfrac{m}{s^{2}}$ với biên độ góc $\Large \alpha_{0}$. Thời gian ngắn nhất vật đi từ vị trí biên dương đến vị trí có li độ góc $\Large \alpha=\dfrac{\alpha_{0}}{\sqrt{2}}$ gần giá trị nào nhất sau đây?

• A. 0,236 s.
• B. 0,118 s.
• C. 0,355 s
• D. 0,177 s.

Phương pháp: 
Chu kì dao động của con lắc đơn dao động điều hòa: $\Large T=2 \pi \sqrt{\frac{l}{g}}$
Sử dụng VTLG. 
Cách giải: 
Chu kì dao động: $\Large T=2 \pi \sqrt{\frac{l}{g}}=2 \pi \sqrt{\frac{0,5}{9,8}}=1,42 s$
Biểu diễn các vị trí trên VTLG: 

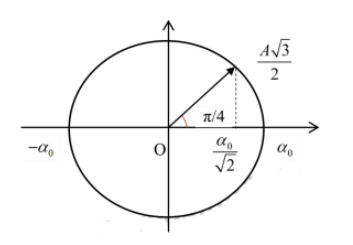
Từ VTLG ta thấy góc quét được là: $\Large \alpha=\dfrac{\pi}{4}$
$\Large \Rightarrow$ Thời gian ngắn nhất vật đi từ vị trí biên dương đến vị trí có li độ góc $\Large \alpha=\dfrac{\alpha_{0}}{\sqrt{2}}$ là: 

$\Large \Delta t=\dfrac{\alpha}{\omega}=\alpha \cdot \dfrac{T}{2 \pi}=\dfrac{\pi}{4} \cdot \dfrac{T}{2 \pi}=\dfrac{T}{8}=\dfrac{1,42}{8}=0,177 s$

Chọn D.