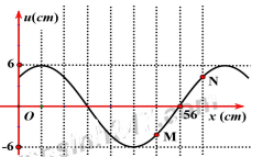
Một sóng hình sin lan truyền trên một sợi dây đàn hồi theo chiều từ M

Một sóng hình sin lan truyền trên một sợi dây đàn hồi theo chiều từ M đến O. Hình vẽ bên mô tả hình dạng của sợi dây tại thời điểm $\Large t_{1}$. Cho tốc độ truyền sóng trên dây bằng 64 cm/s. Vận tốc của điểm N tại thời điểm $\Large t_{2}=t_{1}+\frac{1}{3} s$ gần đúng với giá trị nào nhất sau đây?

• A. - 9,76 cm/s.
• B. 26,66 cm/s.
• C. 36,41 cm/s. 
• D. - 36,41 cm/s.

Phương pháp: 
Độ lệch pha giữa M và N: $\Large \Delta \varphi=\dfrac{2 \pi d}{\lambda}$
Sử dụng kĩ năng đọc đồ thị và VTLG. 
Cách giải: 
Từ đồ thị ta thấy 7 ô tương ứng với 56cm, vậy 1 ô tương ứng với 8cm. 
Một bước sóng tương ứng với 8 ô. Vậy: $\Large \lambda=8.8=64 cm$
Có $\Large v=64 cm \Rightarrow T=\dfrac{\lambda}{v}=\dfrac{64}{64}=1 s \Rightarrow \omega=2 \pi rad / s$
Khoảng cách MN theo phương truyền sóng tương ứng 2 ô nên độ lệch pha của M và N là: 

$\Large \Delta \varphi=\dfrac{2 \pi d}{\lambda}=\dfrac{2 \pi \cdot \dfrac{\lambda}{4}}{\lambda}=\dfrac{\pi}{2}$

Góc quét được sau $\Large \dfrac{1}{3} s$ là: $\Large \alpha=\omega . \Delta t=2 \pi \cdot \dfrac{1}{3}=\dfrac{2 \pi}{3} rad =120^{\circ}$
Biểu diễn M và N tại $\Large t_{1} \text { và } t_{2}$ trên VTLG: 

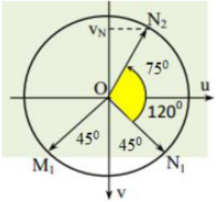
Từ VTLG ta có: $\Large v_{N}\left(t_{2}\right)=-A \omega . \sin 75=-6.2 \pi . \sin 75=-36,41 cm / s$
Chọn D.