Trên mặt nước có hai nguồn sóng kết hợp A và B cách nhau 13cm, dao độn

MỤC LỤC
Câu hỏi:
Trên mặt nước có hai nguồn sóng kết hợp A và B cách nhau 13cm, dao động cùng pha, cùng biên độ a theo phương thẳng đứng. Điểm O thuộc mặt nước cách A và B lần lượt là 5 cm và 12 cm dao động với biên độ là 2a. Điểm M thuộc đoạn AB, gọi (d) là đường thẳng đi qua O và M. Cho M di chuyển trên đoạn AB đến vị trí sao cho tổng khoảng cách từ hai nguồn đến đường thẳng (d) là lớn nhất thì phần tử nước tại M dao động với biên độ 2a. Xét trong khoảng AB tối thiểu có số điểm dao động với biên độ 2a là
Đáp án án đúng là: C
Lời giải chi tiết:
Phương pháp:
Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha: d2−d1=kλ;k∈Z
Số cực đại giao thoa bằng số giá trị k nguyên thỏa mãn: −ABλ<k<ABλ
Cách giải:
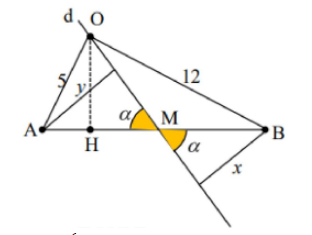
Ta có: {y=AM⋅sinαx=BM⋅sinα⇒x+y=(AM+BM)⋅sinα=15⋅sinα
(x+y)max=15⇔sinα=1⇔α=90∘
Vậy M≡H⇒{HA=2513cmHB=14413cm⇒{OA−OB=kHA−HB=mλ
km=OA−OBHA−HB=713⇒{k=−7m=−13⇒λ=713cm
Số cực đại giao thoa trên AB bằng số giá trị n nguyên thỏa mãn:
−ABλ<n<ABλ⇔−13713<k<13713 ⇔−24,1<k<24,1⇒k=−24;−23;…;24
Có 49 giá trị của n, vậy có 49 điểm dao động với biên độ cực đại.
Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Đặt điện áp u=U√2cos(100t)(V) vào hai đầu đoạn mạc
- Một máy phát điện xoay chiều một pha có rôto là một nam châm điện có m
- Trong các thí nghiệm sau đây, thí nghiệm nào có thể sử dụng để đo bước
- Chiếu xiên một chùm sáng hẹp (coi như một tia sáng) gồm hai ánh sáng đ
- Chiếu một tia sáng trắng tới mặt bên của một lăng kính sao cho tồn tại