Một chất điểm đang dao động điều hòa với phương trình $\Large x=2 \cos

Một chất điểm đang dao động điều hòa với phương trình $\Large x=2 \cos \left(2 \pi t+\dfrac{\pi}{4}\right) cm$. Tính từ thời điểm ban đầu, chất điểm đi qua vị trí có vận tốc bằng $\Large -2 \pi cm / s$ lần thứ 2020 vào thời điểm

• A. $\Large \dfrac{24241}{24} s$
• B. $\Large \dfrac{12119}{24} s$
• C. $\Large \dfrac{24239}{24} s$
• D. $\Large \dfrac{12121}{24} s$

Phương pháp: 
Phương trình của li độ và vận tốc: $\Large \left\{\begin{array}{l}
x=A \cos (\omega t+\varphi) \\
v=\omega A \cdot \cos \left(\omega t+\varphi+\dfrac{\pi}{2}\right)
\end{array}\right.$
Sử dụng VTLG cho vận tốc và công thức $\Large \Delta t=\dfrac{\alpha}{\omega}=\alpha \cdot \dfrac{T}{2 \pi}$
Cách giải: 
Chu kì: $\Large T=\dfrac{2 \pi}{\omega}=\dfrac{2 \pi}{2 \pi}=1 s$
Ta có: $\Large x=2 \cos \left(2 \pi t+\dfrac{\pi}{4}\right) cm \Rightarrow v=4 \pi \cdot\left(2 \pi t+\dfrac{3 \pi}{4}\right) cm / s$
Trong 1 chu kì vật đi qua vị trí có vận tốc bằng $\Large -2 \pi cm/s$
Sau 1009T vật đi qua vị trí có vận tốc bằng $\Large -2 \pi cm/s$ lần thứ 2018. 
Biểu diễn trên VTLG. 

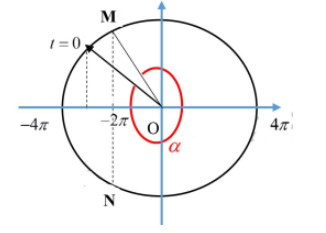
Sau 1009T vật qua vị trí có vận tốc $\Large -2 \pi cm/s$ khi góc quét bằng: $\Large \alpha=\dfrac{\pi}{4}+\pi+\dfrac{\pi}{2}+\dfrac{\pi}{6}=\dfrac{23 \pi}{12}$

$\Large \Rightarrow \Delta t=\alpha \cdot \dfrac{T}{2 \pi}=\dfrac{23 \pi}{12} \cdot \dfrac{T}{2 \pi}=\dfrac{23 T}{24}$

 Tính từ thời điểm ban đầu, chất điểm đi qua vị trí có vận tốc bằng $\Large -2 \pi cm/s$ lần thứ 2020 vào thời điểm: 

$\Large t=1009 T+\Delta t=1009.1+\dfrac{23.1}{24}=\dfrac{24239}{24} s$
 

Chọn C.