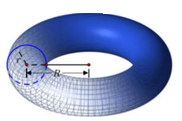
Một cái phao có kích thước như hình vẽ. Tính thể tích hình đó theo $\L

Một cái phao có kích thước như hình vẽ. Tính thể tích hình đó theo $\Large\mathrm{R}$ và $\Large\mathrm{r}$.

• A.

  $\Large\mathrm{V=2 \pi^{2} r^{2} R}$

• B.

  $\Large\mathrm{V=2 \pi^{2} r R^{2}}$

• C.

  $\Large\mathrm{V=\pi^{2} r R^{2}}$

• D.

  $\Large\mathrm{V=\pi^{2} r^{2} R}$

Gắn hệ trục tọa độ như hình vẽ:
 
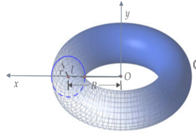
Ta có phương trình đường tròn là: $\Large\mathrm{(x-R)^{2}+y^{2}=r^{2}}$
$\Large\mathrm{\Rightarrow x=R \pm \sqrt{r^{2}-y^{2}}}$
$\Large\mathrm{V=\pi \int\limits_{-r}^{r}\left[\left(R+\sqrt{r^{2}-y^{2}}\right)^{2}-\left(R-\sqrt{r^{2}-y^{2}}\right)^{2}\right] d y}$
$\Large\mathrm{=\pi \int\limits_{-r}^{r}4 \mathrm{R} \sqrt{r^{2}-y^{2}} d y }.$ Đặt $\Large\mathrm{y=\mathrm{rsint} \Leftrightarrow d y=r \cos t d t .}$ Đổi cận $\Large -r \rightarrow \dfrac{-\pi}{2} ; r \rightarrow \dfrac{\pi}{2}$
$\Large\Rightarrow V=\pi\int\limits_{-\dfrac{\pi}{2}}^{\dfrac{\pi}{2}} 4 \mathrm{R} \sqrt{r^{2}\left(1-\sin ^{2} t\right)}. r \cos t d t=\pi\int\limits_{-\dfrac{\pi}{2}}^{\dfrac{\pi}{2}}4 \mathrm{R.} r^{2} \cos ^{2} t d t\\\Large =2 \pi^{2} r^{2} R$