Một bồn nước được thiết kế với chiều cao 8 dm , miệng bồn nước là hình

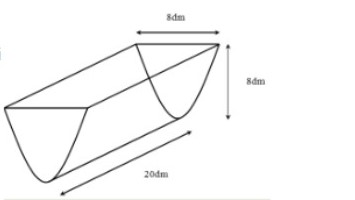
Một bồn nước được thiết kế với chiều cao 8 dm , miệng bồn nước là hình chữ nhật có chiều dài 20 dm , chiều rộng 8 dm và bề mặt cong đều nhau với mặt cắt ngang là một hình parabol như hình vẽ bên . Hỏi bồn chứa được tối đa bao nhiêu lít nước ?

• A.

  A. $\Large \dfrac{1280}{3}(lit)$

• B.

  B. $\Large 1280\pi (lit)$

• C.

  C. $\Large \dfrac{2560}{3}(lit)$

• D.

  D. $\Large 1280(lit)$

Phương trình parabol (P) có dạng $\Large y=a{{x}^{2}}$ với $\Large a>0$ .

Ta thấy (P) đi qua các điểm (-4;8) và (4;8) nên $\Large a=\dfrac{1}{2}$

Suy ra phương trình parabol (P) là $\Large y=\dfrac{1}{2}{{x}^{2}}$

Diện tích mặt cắt parabol của bồn nước cùng chính là diện tích của hình phẳng được giới hạn bởi các đường $\Large y=\dfrac{1}{2}{{x}^{2}}$ và $\Large y=8$ .

Diện tích đó là : $\Large S=\int\limits_{-4}^{4}{\left| \dfrac{1}{2}{{x}^{2}}-8 \right|dx=\int\limits_{-4}^{4}{\left( 8-\dfrac{1}{2}{{x}^{2}} \right)dx=\dfrac{128}{3}(d{{m}^{2}})}}$

Do đó thể tích của bồn nước là : $\Large V=\dfrac{2560}{3}d{{m}^{3}}$