Một bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành k
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Một bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường y=√x+1y=√x+1 và trục OxOx quay quanh trục OxOx biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
r1=y1=1⇒x1=0r1=y1=1⇒x1=0
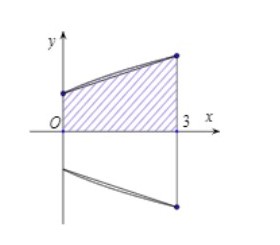
r2=y2=2⇒x2=3r2=y2=2⇒x2=3
Suy ra: V=π3∫0y2dx=π3∫0(x+1)dx=V=π3∫0y2dx=π3∫0(x+1)dx= π(x22+x)|30=152π
Xem thêm các bài tiếp theo bên dưới
- Một xe lửa chuyển động chậm dần đều và dừng hẳn sau 20 giây kể từ khi
- Biết F(x) là một nguyên hàm của hàm số $\Large f(x)=\dfrac{{{
- Một ô tô bắt đầu chuyển động nhanh dần đều với gia tốc $\Large {{a}_{1
- Tích phân $\Large I=\int\limits_{0}^{\dfrac{\pi }{4}}{\dfrac{2x-\sin x
- Cho tích phân $\Large I=\int\limits_{e}^{{{e}^{2}}}{\dfrac{({{x}^{2}}+