Mạch dao động LC có tụ phẳng không khí hình tròn bán kính 48cm, cách n

Mạch dao động LC có tụ phẳng không khí hình tròn bán kính 48cm, cách nhau 4cm phát ra sóng điện từ bước sóng 100m. Nếu đưa vào giữa hai bản tụ tấm điện môi phẳng song song và cùng kích thước với hai bản có hằng số điện môi $\varepsilon $ = 7, bề dày 2cm thì phát ra sóng điện từ bước sóng là

• A. 100m
• B. 100$\sqrt{2}$m
• C. 132,29m
• D. 175m

Giải: Điện dung của tụ không khí ban đầu    $C_o$ = $\frac{\pi {{R}^{2}}}{{{9.10}^{9}}.4\pi {{d}_{0}}}=\frac{{{R}^{2}}}{{{36.10}^{9}}.{{d}_{o}}}$ 

( R = 48cm, $d_o$ = 4cm)

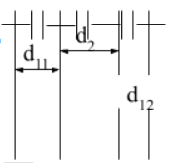
  Khi đưa tấm điện môi vào giữa hai bản tụ thì bộ tụ gồm tụ không khí C1 với khoảng cách giữa hai bản tụ $d_1$ = $d_o$-$d_2$ = 2cm, nối tiếp với tụ $C_2$ có hằng số điện môi $\varepsilon$ = 7. $d_2$ = 2cm

  $C_1$ = $\frac{\pi {{R}^{2}}}{{{9.10}^{9}}.4\pi {{d}_{1}}}=\frac{{{R}^{2}}}{{{36.10}^{9}}.{{d}_{1}}}$= 2$C_o$  

$C_2$ =$\frac{\varepsilon \pi {{R}^{2}}}{{{9.10}^{9}}.4\pi {{d}_{2}}}=\frac{\varepsilon {{R}^{2}}}{{{36.10}^{9}}.{{d}_{2}}}$= 14$C_o$

  Điện dung tương đương của bộ tụ C = $\frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}=\frac{7}{4}{{C}_{0}}$

  Bước sóng do mạch phát ra:    ${{\lambda }_{o}}$ = $2\pi c\sqrt{L{{C}_{0}}}$ = 100m   $\lambda =2\pi \sqrt{LC}$

$\frac{\lambda }{{{\lambda }_{0}}}=\sqrt{\frac{C}{{{C}_{0}}}}=\sqrt{\frac{7}{4}}$=1,322876 => $\lambda $ = 132,29m. Chọn đáp án C.