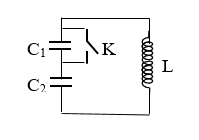
Một mạch dao động gồm cuộn thuần cảm L và hai tụ $\Large C_1=2C_2$ mắc

Một mạch dao động gồm cuộn thuần cảm L và hai tụ $\Large C_1=2C_2$ mắc nối tiếp (hình vẽ ). Mạch đang hoạt động thì ta đóng khóa K ngay tại thời điểm năng lượng trong cuộn cảm triệt tiêu. Năng lượng toàn phần của mạch sau đó sẽ

• A.

  không đổi.

• B.

  giảm còn 1/3.

• C.

  giảm còn 2/3.

• D.

  giảm còn 4/9.

Giải:  Gọi $\large Q_o$ là điện tích cực đại trong mạch

Năng lượng ban đầu của mạch:

$W_o$ = $\frac{Q_{0}^{2}}{2C}$= $\frac{3Q_{0}^{2}}{2{{C}_{1}}}$=$\frac{3Q_{0}^{2}}{4{{C}_{2}}}$(*)

Khi năng lượng cuộn cảm triệt tiêu $\large q = Q_0$

$W_o$  = $W_1$  + $W_2$ với  $W_2$  = $\frac{Q_{0}^{2}}{2{{C}_{2}}}$.

Khi đóng khóa K thi năng lượng toàn phần của mạch: W = $W_2$ = $\frac{Q_{0}^{2}}{2{{C}_{2}}}$ (**)

Từ đó suy ra: $\frac{W}{{{W}_{0}}}$= $\frac{2}{3}$ => W = $\frac{2}{3}$$W_o$   

Chọn đáp án C