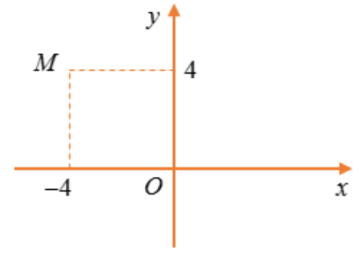
Điểm $\Large M$ trong hình vẽ bên là điểm biểu diễn số phức $\Large z.

Điểm $\Large M$ trong hình vẽ bên là điểm biểu diễn số phức $\Large z.$

Tính mô-đun của số phức $\Large w=\bar{z}+iz$

 

• A.

  A. $\Large |w|=\sqrt{28}.$

• B.

  B. $\Large |w|=\sqrt{182}.$

• C.

  C. $\Large |w|=\sqrt{128}.$

• D.

  D. $\Large |w|=\sqrt{12}.$

Chọn C

Số phức có dạng: $\Large z=a+bi.$ Điểm $\Large M (a; b)$ trong hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức $\Large z=a+bi.$

Theo điểm biểu diễn ở trên điểm $\Large M(-4; 4)$ là điểm biểu diễn của số phức: $\Large z=-4+4i.$

Ta cũng suy ra được số phức liên hợp của $\Large z$ là $\Large \bar{z}=-4-4i.$

Do đó: $\Large w=\bar{z}+iz=-4-4i+i(-4+4i)=-8-8i.$

Vậy mô-đun của số phức $\Large w$ là: $\Large |w|=\sqrt{(-8)^2+(-8)^2}=\sqrt{128}.$